题目内容
2.已知函数f(x)=cos($\frac{4π}{3}$-2x)+2cos2x(1)求f(x)的最大值,并写出使f(x)取得最大值时对应的x的集合.
(2)若把函数f(x)的图象向右平移$\frac{π}{4}$个单位长度后得到函数g(x)的图象,求函数g(x)的单调递减区间.
分析 (1)由三角函数中的恒等变换应用化简函数解析式可得f(x)=cos(2x+$\frac{π}{3}$)+1,利用余弦函数的图象和性质即可得解.
(2)根据函数y=Asin(ωx+φ)的图象变换得g(x)=cos(2x-$\frac{π}{6}$)+1,由2kπ≤2x-$\frac{π}{6}$≤2kπ+π,可得函数g(x)的单调递减区间.
解答 (本小题满分10分)
解:(1)f(x)=cos($\frac{4π}{3}$-2x)+2cos2x
=$\frac{1}{2}$cos2x-$\frac{\sqrt{3}}{2}$sin2x+1
=cos(2x+$\frac{π}{3}$)+1
∵x∈R,
∴f(x)max=2
当2x+$\frac{π}{3}$=2kπ,即x=kπ-$\frac{π}{6}$时,f(x)取得最大值,由此可得使f(x)取得最大的x的集合是:{x|x=kπ-$\frac{π}{6}$,k∈Z}
(2)根据平移变换,得
g(x)=f(x-$\frac{π}{4}$)=cos(2x-$\frac{π}{6}$)+1
由2kπ≤2x-$\frac{π}{6}$≤2kπ+π,得 kπ+$\frac{π}{12}$≤x≤kπ+$\frac{7π}{12}$,
所以函数g(x)的单调递减区间是[kπ+$\frac{π}{12}$,kπ+$\frac{7π}{12}$],k∈Z.
点评 本题主要考查了三角函数中的恒等变换应用,函数y=Asin(ωx+φ)的图象变换,余弦函数的图象和性质,属于基本知识的考查.

练习册系列答案
相关题目
17.设全集U={1,2,3,4,5,6,7,8,9},集合A={1,3,5,7,9},B={1,2,3,4,5},则(∁UA)∩B=( )
| A. | {1,3,5} | B. | {1,2,3,4,5} | C. | {7,9} | D. | {2,4} |
11.某公共汽车站每隔10分钟有一辆汽车到达,乘客到达车站的时刻是任意的,则一个乘客候车时间不超过7分钟的概率是( )
| A. | $\frac{1}{10}$ | B. | $\frac{3}{10}$ | C. | $\frac{5}{10}$ | D. | $\frac{7}{10}$ |
12.如图是函数f(x)=x3+bx2+cx+d的大致图象,则x1+x2=( )
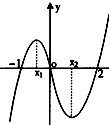

| A. | $\frac{2}{3}$ | B. | $\frac{10}{9}$ | C. | $\frac{8}{9}$ | D. | $\frac{28}{9}$ |