题目内容
已知圆C的圆心与圆O：x2+y2=1的圆心关于直线l：x+y-2=0对称，且圆C与直线l相切，则圆C的方程为________．
（x-2）2+（y-2）2=2
分析：设出对称圆的圆心坐标，利用圆C的圆心与圆O：x2+y2=1的圆心关于直线l：x+y-2=0对称，求出对称圆的圆心坐标，然后利用圆心到直线的距离求出对称圆的半径，即可求出对称圆的方程．
解答：设圆C的圆心（a，b），因为圆C的圆心与圆O：x2+y2=1的圆心关于直线l：x+y-2=0对称，
所以
，解得a=2，b=2；
又因为圆C与直线l相切，则圆C的半径为：
=
，
所以所求圆的方程为：（x-2）2+（y-2）2=2．
故答案为：（x-2）2+（y-2）2=2．
点评：本题是中档题，考查圆心关于直线对称圆的圆心的求法，点到直线的距离公式的应用，考查计算能力．
分析：设出对称圆的圆心坐标，利用圆C的圆心与圆O：x2+y2=1的圆心关于直线l：x+y-2=0对称，求出对称圆的圆心坐标，然后利用圆心到直线的距离求出对称圆的半径，即可求出对称圆的方程．
解答：设圆C的圆心（a，b），因为圆C的圆心与圆O：x2+y2=1的圆心关于直线l：x+y-2=0对称，
所以
，解得a=2，b=2；又因为圆C与直线l相切，则圆C的半径为：
=，所以所求圆的方程为：（x-2）2+（y-2）2=2．
故答案为：（x-2）2+（y-2）2=2．
点评：本题是中档题，考查圆心关于直线对称圆的圆心的求法，点到直线的距离公式的应用，考查计算能力．
练习册系列答案
相关题目
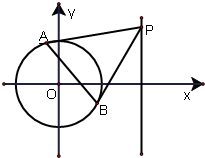已知圆C的圆心为原点O，且与直线
且与直线y=x相切于原点O．椭圆
与圆C的一个交点到椭圆两焦点的距离之和为10．