题目内容
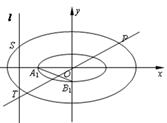
如图,椭圆 与椭圆
与椭圆 中心在原点,焦点均在
中心在原点,焦点均在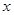 轴上,且离心率相同.椭圆
轴上,且离心率相同.椭圆 的长轴长为
的长轴长为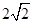 ,且椭圆
,且椭圆 的左准线
的左准线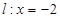 被椭圆
被椭圆 截得的线段
截得的线段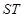 长为
长为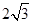 ,已知点
,已知点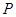 是椭圆
是椭圆 上的一个动点.
上的一个动点.
⑴求椭圆 与椭圆
与椭圆 的方程;
的方程;
⑵设点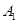 为椭圆
为椭圆 的左顶点,点
的左顶点,点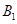 为椭圆
为椭圆 的下顶点,若直线
的下顶点,若直线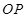 刚好平分
刚好平分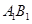 ,求点
,求点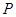 的坐标;
的坐标;
⑶若点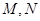 在椭圆
在椭圆 上,点
上,点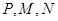 满足
满足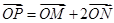 ,则直线
,则直线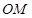 与直线
与直线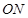 的斜率之积是否为定值?若是,求出该定值;若不是,说明理由.
的斜率之积是否为定值?若是,求出该定值;若不是,说明理由.
 与椭圆
与椭圆 中心在原点,焦点均在
中心在原点,焦点均在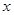 轴上,且离心率相同.椭圆
轴上,且离心率相同.椭圆 的长轴长为
的长轴长为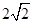 ,且椭圆
,且椭圆 的左准线
的左准线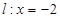 被椭圆
被椭圆 截得的线段
截得的线段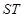 长为
长为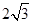 ,已知点
,已知点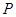 是椭圆
是椭圆 上的一个动点.
上的一个动点.
⑴求椭圆
 与椭圆
与椭圆 的方程;
的方程;⑵设点
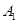 为椭圆
为椭圆 的左顶点,点
的左顶点,点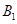 为椭圆
为椭圆 的下顶点,若直线
的下顶点,若直线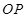 刚好平分
刚好平分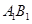 ,求点
,求点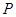 的坐标;
的坐标;⑶若点
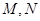 在椭圆
在椭圆 上,点
上,点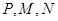 满足
满足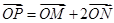 ,则直线
,则直线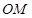 与直线
与直线 的斜率之积是否为定值?若是,求出该定值;若不是,说明理由.
的斜率之积是否为定值?若是,求出该定值;若不是,说明理由.(1)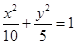 ,(2)
,(2) ,(3)
,(3)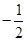 .
.
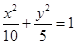 ,(2)
,(2) ,(3)
,(3)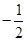 .
.试题分析:(1)求椭圆方程,基本方法是待定系数法.关键是找全所需条件. 椭圆中
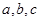 三个未知数的确定只需两个独立条件,根据椭圆
三个未知数的确定只需两个独立条件,根据椭圆 的长轴长为
的长轴长为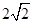 得
得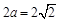 ,又由椭圆
,又由椭圆 的左准线
的左准线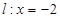 得
得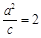 ,所以
,所以 ,
,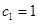 ,
,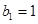 ,就可得到椭圆
,就可得到椭圆 的标准方程;由椭圆
的标准方程;由椭圆 与椭圆
与椭圆 离心率相同,得
离心率相同,得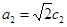 再由椭圆
再由椭圆 过点
过点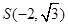 ,代入可得椭圆
,代入可得椭圆
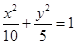 (2)涉及弦中点问题,一般用“点差法”构造等量关系.本题较简单,可直接求出
(2)涉及弦中点问题,一般用“点差法”构造等量关系.本题较简单,可直接求出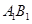 中点坐标,再利用直线
中点坐标,再利用直线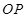 与椭圆
与椭圆 联立方程组求交点坐标;(3)求定值问题,一是确定定值,这可利用特殊情况給于确定,二是参数选择,不仅要揭示问题本质,更要易于消元,特别是整体消元.本题研究的是直线
联立方程组求交点坐标;(3)求定值问题,一是确定定值,这可利用特殊情况給于确定,二是参数选择,不仅要揭示问题本质,更要易于消元,特别是整体消元.本题研究的是直线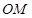 与直线
与直线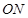 的斜率之积,即它们坐标满足
的斜率之积,即它们坐标满足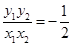 为定值,参数选为点
为定值,参数选为点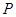 的坐标,利用点
的坐标,利用点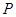 的坐标满足
的坐标满足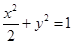 进行整体消元.
进行整体消元.试题解析:⑴设椭圆
 方程为
方程为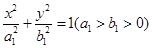 ,椭圆
,椭圆 方程为
方程为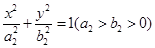 ,
,则
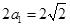 ,∴
,∴ ,又其左准线
,又其左准线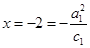 ,∴
,∴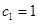 ,则
,则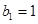
∴椭圆
 方程为
方程为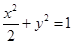 ,其离心率为
,其离心率为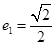 , 3分
, 3分∴椭圆
 中
中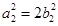 ,由线段的
,由线段的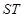 长为
长为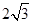 ,得
,得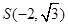 ,代入椭圆
,代入椭圆
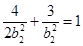 ,
,得
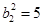 ,∴
,∴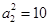 ,椭圆
,椭圆 方程为
方程为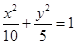 ; 6分
; 6分⑵
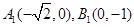 ,则
,则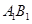 中点为
中点为 ,∴直线
,∴直线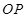 为
为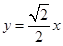 , 7分
, 7分由
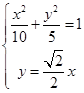 ,得
,得 或
或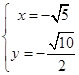 ,
, ∴点
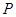 的坐标为
的坐标为 ; 10分
; 10分⑶设
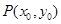 ,
,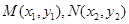 ,则
,则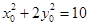 ,
,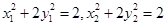 ,
,由题意
 ,∴
,∴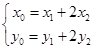 12分
12分∴

 14分
14分∴
 ,∴
,∴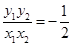 ,即
,即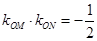 ,
,∴直线
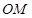 与直线
与直线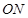 的斜率之积为定值,且定值为
的斜率之积为定值,且定值为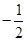 . 16分
. 16分
练习册系列答案
相关题目
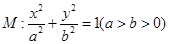 的离心率为
的离心率为 ,且过点
,且过点 直线
直线 与椭圆M交于A、C两点,直线
与椭圆M交于A、C两点,直线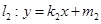 与椭圆M交于B、D两点,四边形ABCD是平行四边形
与椭圆M交于B、D两点,四边形ABCD是平行四边形 、
、 ,动点
,动点 满足:
满足: ,且
,且
 的方程;
的方程; 的切线
的切线 与轨迹
与轨迹 .
.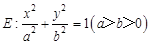 ,斜率为1的直线不经过原点
,斜率为1的直线不经过原点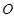 ,而且与椭圆相交于
,而且与椭圆相交于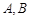 两点,
两点,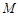 为线段
为线段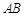 的中点.
的中点. 与
与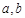 之间满足什么关系;若不能,说明理由;
之间满足什么关系;若不能,说明理由; 的中点,且
的中点,且 点在椭圆上.若
点在椭圆上.若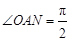 ,求椭圆的离心率.
,求椭圆的离心率. 的顶点在坐标原点
的顶点在坐标原点 ,对称轴为
,对称轴为 轴,焦点为
轴,焦点为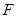 ,抛物线上一点
,抛物线上一点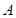 的横坐标为2,且
的横坐标为2,且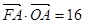 .
.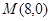 作直线
作直线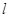 交抛物线于
交抛物线于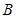 ,
,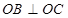 .
.
 的离心率为
的离心率为 ,直线
,直线 与圆
与圆 相切.
相切. 的方程;
的方程; 与椭圆
与椭圆 ,求弦长
,求弦长 .
.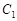 的极坐标方程为
的极坐标方程为 ,曲线
,曲线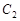 的极坐标方程为
的极坐标方程为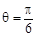 ,曲线
,曲线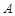 、
、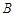 两点.(
两点.(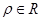 )
)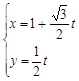 (
(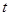 为参数)分别相交于
为参数)分别相交于 两点,求线段
两点,求线段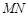 的长度.
的长度.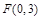 的距离与它到直线y+3=0的距离相等,则P的轨迹方程为 ( )
的距离与它到直线y+3=0的距离相等,则P的轨迹方程为 ( )
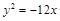
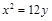
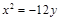
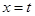 交抛物线
交抛物线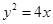 于
于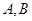 两点.若该抛物线上存在点
两点.若该抛物线上存在点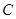 ,使得
,使得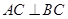 ,则
,则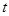 的取值范围为_________.
的取值范围为_________.