题目内容
一个盒子里装有n-1个白球,1个红球,每次随机地取出一个球,若取到白球则放回再取,若取到红球则停止取球,则取球次数ξ的数学期望为__________________________.
解析：ξ可以取1,2,3,…,n,
P(ξ=k)=
(k=1,2,…,n),
∴Eξ=
(1+2+3+…+n)=
.
答案：
练习册系列答案
考前必练系列答案
相关题目
（本小题满分13分）
随机变量X的分布列如下表如示，若数列
是以
为首项，以
为公比的等比数列，则称随机变量X服从等比分布，记为Q(,)．现随机变量X∽Q(
,2)．
| X | 1 | 2 | … | n |
 | |  | … |  |
（Ⅱ）一个盒子里装有标号为1，2，…，n且质地相同的标签若干张，从中任取1张标签所得的标号为随机变
量X．现有放回的从中每次抽取一张，共抽取三次，求恰好2次取得标签的标号不大于3的概率．
（本小题满分13分）
随机变量X的分布列如下表如示，若数列
是以
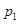为首项，以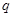
为公比的等比数列，则称随机变量X服从等比分布，记为Q(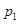,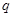)．现随机变量X∽Q(
,2)．
|
X |
1 |
2 |
… |
n |
|
|
|
|
… |
|
(Ⅰ)求n 的值并求随机变量X的数学期望EX；
（Ⅱ）一个盒子里装有标号为1，2，…，n且质地相同的标签若干张，从中任取1张标签所得的标号为随机变量X．现有放回的从中每次抽取一张，共抽取三次，求恰好2次取得标签的标号不大于3的概率．