题目内容
若f(x)具有性质:①f(x)为偶函数,②对任意x∈R,都有f( -x)=f(
-x)=f( +x),则f(x)的解析式可以是 .(只写一个即可)
+x),则f(x)的解析式可以是 .(只写一个即可)
【答案】分析:题目中条件:“若f(x)具有性质:①f(x)为偶函数,”说明有f(-x)=f(x);“②对任意x∈R,都有f(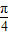 -x)=f(
-x)=f(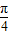 +x)”说明有:f(
+x)”说明有:f(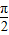 +x)=f(x),是周期函数.
+x)=f(x),是周期函数.
解答:解:∵若f(x)具有性质:①f(x)为偶函数,
∴说明有f(-x)=f(x);
∵②对任意x∈R,都有f(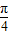 -x)=f(
-x)=f(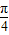 +x)
+x)
∴说明有:f(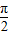 +x)=f(x),是周期函数.
+x)=f(x),是周期函数.
我们从三角函数中寻找即得:f(x)=a或f(x)=cos4x或f(x)=|sin2x|等.
故填:f(x)=a或f(x)=cos4x或f(x)=|sin2x|等.
点评:本题主考查抽象函数的周期性、对称性以及偶函数,抽象函数是相对于给出具体解析式的函数来说的,它虽然没有具体的表达式,但是有一定的对应法则,满足一定的性质,这种对应法则及函数的相应的性质是解决问题的关键.抽象函数的抽象性赋予它丰富的内涵和多变的思维价值,可以考查类比猜测,合情推理的探究能力和创新精神.
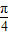 -x)=f(
-x)=f(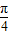 +x)”说明有:f(
+x)”说明有:f(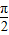 +x)=f(x),是周期函数.
+x)=f(x),是周期函数.解答:解:∵若f(x)具有性质:①f(x)为偶函数,
∴说明有f(-x)=f(x);
∵②对任意x∈R,都有f(
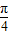 -x)=f(
-x)=f(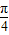 +x)
+x)∴说明有:f(
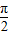 +x)=f(x),是周期函数.
+x)=f(x),是周期函数.我们从三角函数中寻找即得:f(x)=a或f(x)=cos4x或f(x)=|sin2x|等.
故填:f(x)=a或f(x)=cos4x或f(x)=|sin2x|等.
点评:本题主考查抽象函数的周期性、对称性以及偶函数,抽象函数是相对于给出具体解析式的函数来说的,它虽然没有具体的表达式,但是有一定的对应法则,满足一定的性质,这种对应法则及函数的相应的性质是解决问题的关键.抽象函数的抽象性赋予它丰富的内涵和多变的思维价值,可以考查类比猜测,合情推理的探究能力和创新精神.

练习册系列答案
相关题目
 -x)=f(
-x)=f( +x),则f(x)的解析式可以是 .(只写一个即可)
+x),则f(x)的解析式可以是 .(只写一个即可) -x)=f(
-x)=f( +x),则f(x)的解析式可以是 .(只写一个即可)
+x),则f(x)的解析式可以是 .(只写一个即可)