题目内容
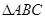 的外接圆半径
的外接圆半径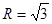 ,角
,角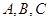 的对边分别是
的对边分别是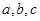 ,且
,且
(1)求角
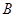 和边长
和边长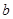 ;
;(2)求
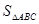 的最大值及取得最大值时的
的最大值及取得最大值时的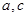 的值,并判断此时三角形的形状.
的值,并判断此时三角形的形状.(1)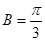 ,
,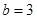 ;(2)
;(2)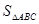 的最大值
的最大值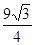 ,此时
,此时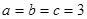 ,此时三角形是等边三角形.
,此时三角形是等边三角形.
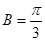 ,
,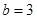 ;(2)
;(2)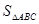 的最大值
的最大值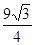 ,此时
,此时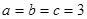 ,此时三角形是等边三角形.
,此时三角形是等边三角形.试题分析:本题主要考查解三角形中的正弦定理或余弦定理的运用,以及基本不等式的运用和求三角形面积的最值.第一问,先利用余弦定理将角化成边,去分母化简,得
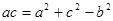 ,再利用余弦定理求
,再利用余弦定理求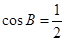 ,在
,在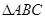 中,
中,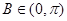 ,所以
,所以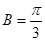 ,再利用正弦定理求边
,再利用正弦定理求边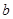 ;第二问,先通过余弦定理
;第二问,先通过余弦定理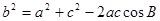 ,再结合基本不等式求出
,再结合基本不等式求出 的最大值,得到面积的最大值,注意等号成立的条件,通过这个条件得出
的最大值,得到面积的最大值,注意等号成立的条件,通过这个条件得出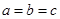 ,所以判断三角形形状为等边三角形.
,所以判断三角形形状为等边三角形.试题解析:(1)由
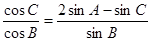 ,得:
,得: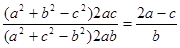 ,
,即
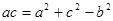 ,所以
,所以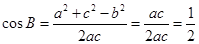 , 4分
, 4分又
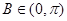 ,所以
,所以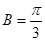 ,又
,又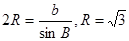 ,所以
,所以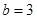 6分
6分(2)由
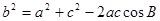 ,
,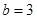 ,
,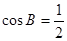
得
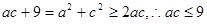
 (当且仅当
(当且仅当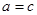 时取等号) 8分
时取等号) 8分所以,
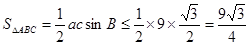 (当且仅当
(当且仅当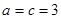 时取等号) 10分
时取等号) 10分此时
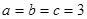
综上,
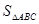 的最大值
的最大值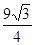 ,取得最大值时,此时三角形是等边三角形. 12分
,取得最大值时,此时三角形是等边三角形. 12分
练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,设S为△ABC的面积,满足
,设S为△ABC的面积,满足 .
. ,且
,且 ,求
,求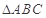 中,已知角
中,已知角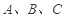 的对边分别为
的对边分别为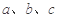 .向量
.向量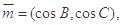
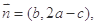 且向量
且向量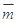 与
与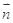 共线.
共线.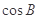 的值;
的值;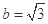 ,求
,求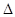 ABC的内角
ABC的内角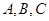 的对边
的对边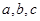 若a=csinA则
若a=csinA则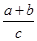 的最大值为( )
的最大值为( )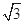
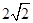
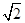
 ,b=
,b= ,则B=
,则B=  的内角
的内角 所对的边长分别为
所对的边长分别为 ,且
,且 ,则边长
,则边长 .
. 中,若
中,若 ,
, ,
, ,则
,则 的大小为_________.
的大小为_________. 中,若
中,若 =
= °, ∠B=
°, ∠B= °,BC =
°,BC = ,则AC =
,则AC =