题目内容
已知幂函数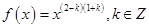 ,且
,且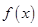 在
在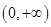 上单调递增.
上单调递增.
(1)求实数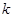 的值,并写出相应的函数
的值,并写出相应的函数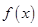 的解析式;
的解析式;
(2)若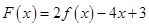 在区间
在区间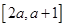 上不单调,求实数
上不单调,求实数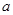 的取值范围;
的取值范围;
(3)试判断是否存在正数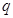 ,使函数
,使函数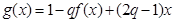 在区间
在区间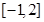 上的值域为
上的值域为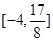 若存在,求出
若存在,求出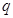 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
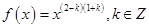 ,且
,且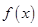 在
在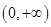 上单调递增.
上单调递增.(1)求实数
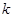 的值,并写出相应的函数
的值,并写出相应的函数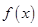 的解析式;
的解析式;(2)若
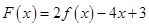 在区间
在区间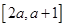 上不单调,求实数
上不单调,求实数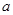 的取值范围;
的取值范围;(3)试判断是否存在正数
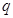 ,使函数
,使函数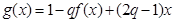 在区间
在区间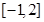 上的值域为
上的值域为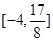 若存在,求出
若存在,求出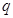 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(1) 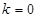 或
或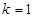 ,
,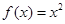 (2)
(2) 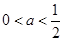 (3)
(3) 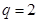
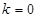 或
或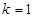 ,
,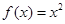 (2)
(2) 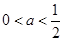 (3)
(3) 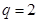
试题分析:(1)由题意知
 ,解得:
,解得: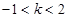 . 2分
. 2分又
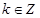 ∴
∴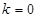 或
或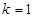 , 3分
, 3分分别代入原函数,得
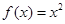 . 4分
. 4分(2)由已知得
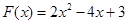 . 5分
. 5分要使函数不单调,则
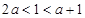 ,则
,则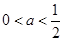 . 8分
. 8分(3)由已知,
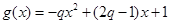 . 9分
. 9分法一:假设存在这样的正数
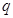 符合题意,
符合题意,则函数
 的图象是开口向下的抛物线,其对称轴为
的图象是开口向下的抛物线,其对称轴为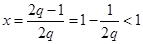 ,
,因而,函数
 在
在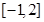 上的最小值只能在
上的最小值只能在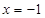 或
或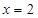 处取得,
处取得,又
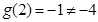 ,
,从而必有
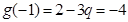 ,解得
,解得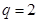 .
.此时,
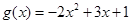 ,其对称轴
,其对称轴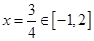 ,
,∴
 在
在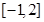 上的最大值为
上的最大值为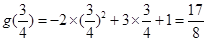 ,符合题意.
,符合题意.∴存在
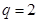 ,使函数
,使函数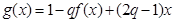 在区间
在区间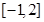 上的值域为
上的值域为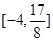 14分法二:假设存在这样的正数
14分法二:假设存在这样的正数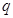 符合题意,
符合题意,由(1)知
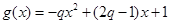 ,
,则函数
 的图象是开口向下的抛物线,其对称轴为
的图象是开口向下的抛物线,其对称轴为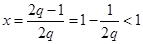 ,
,
点评:第二问中二次函数不单调需满足对称轴在给定区间内,第三问关于最值的考查需注意对称轴与给定区间的关系,从而确定给定区间上的单调性得到最值,一般求解时都要分情况讨论

练习册系列答案
相关题目
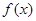 的图像经过
的图像经过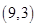 ,则
,则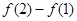 等于( )
等于( )



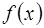 存在反函数,且反函数
存在反函数,且反函数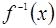 过点(2,4),则
过点(2,4),则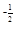 <(3-2a)
<(3-2a)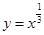 的图像是 ( )
的图像是 ( ) 
 过点
过点 ,则不等式
,则不等式 的解集为__________.
的解集为__________.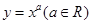 图像经过不等式组
图像经过不等式组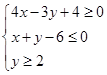 表示的区域,则a的取值范围是
表示的区域,则a的取值范围是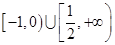


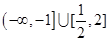
 的图象过点
的图象过点 ,则k+α=_______.
,则k+α=_______.