题目内容
P、Q是抛物线 上两动点,直线
上两动点,直线 分别是C在点P、点Q处的切线,
分别是C在点P、点Q处的切线,
(1)求证:点M的纵坐标为定值,且直线PQ经过一定点;
(2)求 面积的最小值。
面积的最小值。
【答案】
略
【解析】(1)设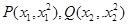 ,中学
,中学
又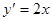
则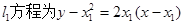
即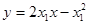 ①
①
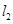 方程为
方程为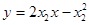 ②中学
②中学
由①②解得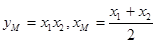 3分
3分
由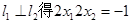 中学
中学
即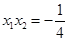
所以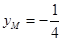 ,
5分
,
5分
PQ方程为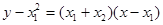
即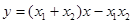
即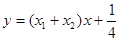 [ 由此得直线PQ一定经过点
[ 由此得直线PQ一定经过点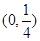 8分
8分
(2)令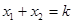 ,
,
则由(1)知点M坐标
直线PQ方程为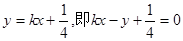 10分
10分
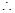 点M到直线PQ距离
点M到直线PQ距离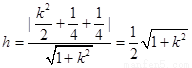
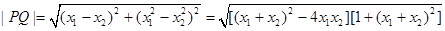
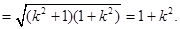 12分
12分
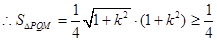 ,
,
当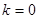 时“=”成立,[
时“=”成立,[
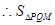 最小值为
最小值为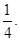

练习册系列答案
相关题目
 直线与抛物线在x轴上方的交点为M,过M作y轴的垂线,垂足为N,O为坐标原点,若四边形OFMN的面积为
直线与抛物线在x轴上方的交点为M,过M作y轴的垂线,垂足为N,O为坐标原点,若四边形OFMN的面积为 .
.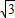 直线与抛物线在x轴上方的交点为M,过M作y轴的垂线,垂足为N,O为坐标原点,若四边形OFMN的面积为
直线与抛物线在x轴上方的交点为M,过M作y轴的垂线,垂足为N,O为坐标原点,若四边形OFMN的面积为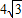 .
.