题目内容
若曲线y=ax2-1上总存在关于直线x+y=0对称的两点,求a的取值范围.
思路解析：充分挖掘隐含条件有两解且关于x+y=0对称,结合图韦达定理求解. 解：与直线x+y=0垂直的直线为y=x+b, 由方程组 Δ=1+4a(b+1)＞0. ① 设关于直线x+y=0对称的两点为A(x1,y1),B(x2,y2). 由韦达定理得x1+x2= 由题设,点( ∴ 将②代入①式得a＞
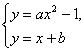消去y,得ax2-x-(b+1)=0.
,y1+y2=(x1+b)+(x2+b)=(x1+x2)+2b=
+2b.
,
)在直线x+y=0上,
=-
-2b,即
=-b,即ab=-1. ②
为所求a的取值范围.
练习册系列答案
小学毕业班总复习系列答案
小学毕业测试卷系列答案
毕业复习指导系列答案
小学毕业考试标准及复习指导系列答案
考前全程总复习系列答案
培优全真模拟试卷系列答案
五读俱全系列答案
同步辅导与能力训练阶段综合测试卷系列答案
小学自评测试
系列答案
相关题目
若曲线y=ax2在点P（1，a）处的切线与直线2x+y-2=0平行，则a=（ ）
A、-
| ||
| B、-1 | ||
| C、1 | ||
D、
|