题目内容
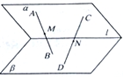（2013•杭州二模）如图，平面α与平面β交于直线l，A，C是平面α内不同点，B，D是平面β内不同的两点，且A，B、C、D不在直线l上，M、N分别是线段AB、CD的中点，下列判断正确的是（ ）分析：A选项，当AB与CD相交，直线AC平行于l时，直线BD可以与l平行；于B选项，当AB，CD是异面直线时，MN不可能与l平行；C选项，若存在异于AB，CD 的直线同时与直线AC，MN，BD都相交，则AB，CD可能是异面直线；D选项，若M，N两点可能重合，则AC∥BD，故AC∥l，此时直线AC与直线l不可能相交．
解答：解：对于A选项，因为AB与CD相交，则ABCD四点共面于平面γ，
且λ∩β=BD，λ∩α=AC，由AC∥l，可得AC∥β，
由线面平行的性质可得AC∥BD，进而可得BD∥l，故A错误；
对于B选项，当AB，CD是异面直线时，MN不可能与l平行，
过N作CD的平行线EF，分别交α，β于E、F，
可得M为EF中点，可得△BMF≌△AME，可得AE∥BF，
显然与题设矛盾，故B错误；
对于C选项，若存在异于AB，CD 的直线同时与直线AC，MN，BD都相交，
则AB，CD可能是异面直线，故C错误；
对于D选项，若M，N两点可能重合，则AC∥BD，故AC∥l，
故此时直线AC与直线l不可能相交，故D正确．
故选D
且λ∩β=BD，λ∩α=AC，由AC∥l，可得AC∥β，
由线面平行的性质可得AC∥BD，进而可得BD∥l，故A错误；
对于B选项，当AB，CD是异面直线时，MN不可能与l平行，
过N作CD的平行线EF，分别交α，β于E、F，
可得M为EF中点，可得△BMF≌△AME，可得AE∥BF，
显然与题设矛盾，故B错误；
对于C选项，若存在异于AB，CD 的直线同时与直线AC，MN，BD都相交，
则AB，CD可能是异面直线，故C错误；
对于D选项，若M，N两点可能重合，则AC∥BD，故AC∥l，
故此时直线AC与直线l不可能相交，故D正确．
故选D
点评：本题考查命题真假的判断与应用，涉及空间中的直线与直线之间的位置关系，属基础题．
练习册系列答案
相关题目