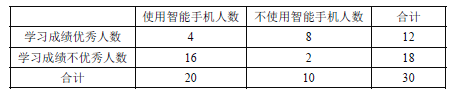
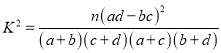题目内容
【题目】已知椭圆![]()
![]() ,
, ![]() 是坐标原点,
是坐标原点, ![]() 分别为其左右焦点,
分别为其左右焦点, ![]() ,
, ![]() 是椭圆上一点,
是椭圆上一点, ![]() 的最大值为
的最大值为![]()
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]()
(i)求证: ![]() 为定值;
为定值;
(ii)求![]() 面积的取值范围.
面积的取值范围.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】试题分析:(1)由椭圆对称性可得M为短轴端点B时![]() 取最大值,因此根据直角三角形
取最大值,因此根据直角三角形![]() 可得
可得![]() ,(2)(i)解几中证明题一般方法为以算代证,先由直线方程与椭圆方程联立,解出
,(2)(i)解几中证明题一般方法为以算代证,先由直线方程与椭圆方程联立,解出![]() 坐标(用直线斜率表示),代入
坐标(用直线斜率表示),代入![]() 可得定值,最后验证斜率不存在的情况也满足(ii)因为
可得定值,最后验证斜率不存在的情况也满足(ii)因为![]() ,所以
,所以![]() 面积为
面积为![]() ,再将(i)
,再将(i)![]() 坐标(用直线斜率表示)代入,得关于直线斜率的一元函数关系,利用基本不等式求最值,确定函数取值范围.
坐标(用直线斜率表示)代入,得关于直线斜率的一元函数关系,利用基本不等式求最值,确定函数取值范围.
试题解析:(1)由题意得![]() ,得椭圆方程为:
,得椭圆方程为: ![]()
(2)
i)当![]() 斜率都存在且不为0时,设
斜率都存在且不为0时,设![]() ,
, ![]()
由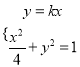 消
消![]() 得
得![]() ,
, ![]()
同理得![]() ,
, ![]()
故![]()
当![]() 斜率一个为0,一个不存在时,得
斜率一个为0,一个不存在时,得![]()
综上得![]() ,得证。
,得证。
ii) 当![]() 斜率都存在且不为0时,
斜率都存在且不为0时,
![]()
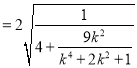
又 ![]()
所以![]()
当![]() 斜率一个为0,一个不存在时,
斜率一个为0,一个不存在时, ![]()
综上得![]()

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
【题目】为大力提倡“厉行节约,反对浪费”,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的列联表:( )
做不到“光盘” | 能做到“光盘” | |
男 | 45 | 10 |
女 | 30 | 15 |
附:
P(K2 | 0.10 | 0.05 | 0.025 |
k | 2.706 | 3.841 | 5.024 |
![]()
参照附表,得到的正确结论是
A.在犯错误的概率不超过l%的前提下,认为“该市居民能否做到‘光盘’与性别有关”
B.在犯错误的概率不超过l%的前提下,认为“该市居民能否做到‘光盘’与性别无关”
C.有90%以上的把握认为“该市居民能否做到‘光盘’与性别有关”
D.有90%以上的把握认为“该市居民能否做到‘光盘’与性别无关”