题目内容
已知向量 =(cosθ,sinθ)与
=(cosθ,sinθ)与 =(cosθ,-sinθ)互相垂直,且θ为锐角,则函数f(x)=sin(2x-θ)的图象的一条对称轴是直线
=(cosθ,-sinθ)互相垂直,且θ为锐角,则函数f(x)=sin(2x-θ)的图象的一条对称轴是直线
- A.x=π
- B.x=

- C.x=

- D.x=

B
分析:由向量 =(cosθ,sinθ)与
=(cosθ,sinθ)与 =(cosθ,-sinθ)互相垂直,得cos2θ-sin2θ=cos2θ=0,由θ为锐角,得
=(cosθ,-sinθ)互相垂直,得cos2θ-sin2θ=cos2θ=0,由θ为锐角,得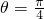 .由函数f(x)=sin(2x-θ)=sin(2x-
.由函数f(x)=sin(2x-θ)=sin(2x- )的对称轴方程为2x-
)的对称轴方程为2x- =k
=k ,k∈Z,知x=
,k∈Z,知x= ,k∈Z,由此能求出结果.
,k∈Z,由此能求出结果.
解答:∵向量 =(cosθ,sinθ)与
=(cosθ,sinθ)与 =(cosθ,-sinθ)互相垂直,
=(cosθ,-sinθ)互相垂直,
∴cos2θ-sin2θ=cos2θ=0,
∵θ为锐角,
∴2θ= ,
,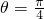 .
.
∴函数f(x)=sin(2x-θ)=sin(2x- )的对称轴方程为2x-
)的对称轴方程为2x- =k
=k ,k∈Z,
,k∈Z,
即x= ,k∈Z,
,k∈Z,
当k=1时,x= ,
,
故选B.
点评:本题考查平面向量的坐标运算,是基础题.解题时要认真审题,注意数量积判断两个平面向量的垂直关系和三角函数性质的应用.
分析:由向量
 =(cosθ,sinθ)与
=(cosθ,sinθ)与 =(cosθ,-sinθ)互相垂直,得cos2θ-sin2θ=cos2θ=0,由θ为锐角,得
=(cosθ,-sinθ)互相垂直,得cos2θ-sin2θ=cos2θ=0,由θ为锐角,得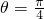 .由函数f(x)=sin(2x-θ)=sin(2x-
.由函数f(x)=sin(2x-θ)=sin(2x- )的对称轴方程为2x-
)的对称轴方程为2x- =k
=k ,k∈Z,知x=
,k∈Z,知x= ,k∈Z,由此能求出结果.
,k∈Z,由此能求出结果.解答:∵向量
 =(cosθ,sinθ)与
=(cosθ,sinθ)与 =(cosθ,-sinθ)互相垂直,
=(cosθ,-sinθ)互相垂直,∴cos2θ-sin2θ=cos2θ=0,
∵θ为锐角,
∴2θ=
 ,
,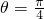 .
.∴函数f(x)=sin(2x-θ)=sin(2x-
 )的对称轴方程为2x-
)的对称轴方程为2x- =k
=k ,k∈Z,
,k∈Z,即x=
 ,k∈Z,
,k∈Z,当k=1时,x=
 ,
,故选B.
点评:本题考查平面向量的坐标运算,是基础题.解题时要认真审题,注意数量积判断两个平面向量的垂直关系和三角函数性质的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知向量
=(cosα,sinα),
=(cosβ,sinβ),若|
-
|=
,则
和
的夹角为( )
| a |
| b |
| a |
| b |
| 2 |
| a |
| b |
| A、60° | B、90° |
| C、120° | D、150° |