题目内容
一名学生练习投篮,每次投篮他投进的概率是 ,共投篮5次.
,共投篮5次.
(1)求他在投篮过程中至少投进1次的概率;
(2)求他在投篮过程中进球数ξ的期望与方差.
解:(1)由于此学生共投篮5次,每一次投篮之间相互不影响,且他一次投篮中投中的概率是 ,故他他在投篮过程中至少投进1次的概率,利用互斥事件的概率公式,得:P=1-
,故他他在投篮过程中至少投进1次的概率,利用互斥事件的概率公式,得:P=1- =
= ;
;
(2)由于随机变量ξ代表的是投篮过程中进球的个数,由题意可知ξ可以等于0,1,2,3,4,5
P(ξ=0)= =
=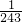 ,
,
P(ξ=1)=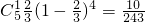 ,
,
P(ξ=2)= ,
,
P(ξ=3)=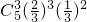 =
= ,
,
P(ξ=4)=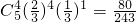 ,
,
P(ξ=5)= ,
,
利用独立重复事件的期望与方差公式可知:Eξ=5× ,Dξ=5×
,Dξ=5× .
.
分析:(1)由题意,由于每次投篮他投进的概率是 ,共投篮5次,并且每次投篮相互之间互不影响,利用相互独立事件的概率公式即可求得;
,共投篮5次,并且每次投篮相互之间互不影响,利用相互独立事件的概率公式即可求得;
(2)由于随机变量ξ代表的是投篮过程中进球的个数,由题意可知ξ可以等于0,1,2,3,4,5;再利用随机变量的定义及期望的定义即可.
点评:此题重点考查了学生理解题意的能力及区别独立事件互斥事件和n次独立重复事件的概率公式及期望与方差的定义及其计算公式.
 ,故他他在投篮过程中至少投进1次的概率,利用互斥事件的概率公式,得:P=1-
,故他他在投篮过程中至少投进1次的概率,利用互斥事件的概率公式,得:P=1- =
= ;
;(2)由于随机变量ξ代表的是投篮过程中进球的个数,由题意可知ξ可以等于0,1,2,3,4,5
P(ξ=0)=
 =
=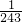 ,
,P(ξ=1)=
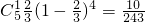 ,
,P(ξ=2)=
 ,
,P(ξ=3)=
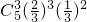 =
= ,
,P(ξ=4)=
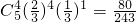 ,
,P(ξ=5)=
 ,
,利用独立重复事件的期望与方差公式可知:Eξ=5×
 ,Dξ=5×
,Dξ=5× .
.分析:(1)由题意,由于每次投篮他投进的概率是
 ,共投篮5次,并且每次投篮相互之间互不影响,利用相互独立事件的概率公式即可求得;
,共投篮5次,并且每次投篮相互之间互不影响,利用相互独立事件的概率公式即可求得;(2)由于随机变量ξ代表的是投篮过程中进球的个数,由题意可知ξ可以等于0,1,2,3,4,5;再利用随机变量的定义及期望的定义即可.
点评:此题重点考查了学生理解题意的能力及区别独立事件互斥事件和n次独立重复事件的概率公式及期望与方差的定义及其计算公式.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
 ,
, 的期望与方差.
的期望与方差.