题目内容
已知随机变量ξ的分布列为下表所示:
| ξ | 1 | 3 | 5 |
| P | 0.4 | 0.1 | x |
- A.3.56
- B.

- C.3.2
- D.
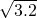
B
分析:先利用期望公式,求得Eξ=3.2,再利用方差公式,求得方差,进而可得ξ的标准差.
解答:由题意,Eξ=1×0.4+3×0.1+5×(1-0.4-0.1)=3.2
∴方差为:(1-3.2)2×0.4+(3-3.2)2×0.1+(5-3.2)2×0.5=1.936+0.004+1.62=3.56
∴ξ的标准差为
故选B.
点评:本题考查知随机变量ξ的期望、方差与标准差,正确运用公式是关键.
分析:先利用期望公式,求得Eξ=3.2,再利用方差公式,求得方差,进而可得ξ的标准差.
解答:由题意,Eξ=1×0.4+3×0.1+5×(1-0.4-0.1)=3.2
∴方差为:(1-3.2)2×0.4+(3-3.2)2×0.1+(5-3.2)2×0.5=1.936+0.004+1.62=3.56
∴ξ的标准差为

故选B.
点评:本题考查知随机变量ξ的期望、方差与标准差,正确运用公式是关键.

练习册系列答案
相关题目
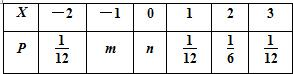 已知随机变量X的分布列如图:其中m,n∈[0,1),且E(X)=
已知随机变量X的分布列如图:其中m,n∈[0,1),且E(X)=| 1 |
| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|