Question

(1)求曲线ρcosθ+1=0关于直线θ=对称的曲线方程.

（2）从极点O引定圆ρ=2cosθ的弦OP，延长OP至Q，使=23，求点Q的轨迹方程.

Answer 1

解：（1）设曲线ρcosθ+1=0上任一点（ρ′，θ′），其关于直线θ=的对称点坐标为（ρ，θ），则ρ′cosθ′+1=0.?

将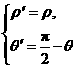代入方程ρ′cosθ′+1=0,得?

ρcos(-θ)+1=0.?

∴ρsinθ+1=0.?

∴所求的曲线方程为ρsinθ+1=0.?

(2)设P(ρ′,θ′),Q(ρ,θ),则ρ′=2cosθ′,?

将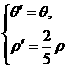代入方程ρ′=2cosθ′,得ρ=2cosθ,即ρ=5cosθ.

∴点Q的轨迹方程为ρ=5cosθ.