Question

（09年丰台区期末理）（14分）

    设椭圆M：(a＞b＞0)的离心率为，长轴长为，设过右焦点F倾

斜角为的直线交椭圆M于A，B两点。

       （Ⅰ）求椭圆M的方程；

（Ⅱ）求证| AB | =；

（Ⅲ）设过右焦点F且与直线AB垂直的直线交椭圆M于C，D，求|AB| + |CD|的最小

值。

Answer 1

解析：（Ⅰ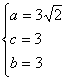）所求椭圆M的方程为…3分

       （Ⅱ）当≠，设直线AB的斜率为k = tan，焦点F ( 3 , 0 )，则直线AB的方程为

              y = k ( x 3 )         有( 1 + 2k² )x² 12k²x + 18( k² 1 ) = 0

              设点A ( x₁ , y₁ ) , B ( x₂ , y₂ )           有x₁ + x₂ =, x₁x₂ =

              |AB| = ** … 6分

              又因为   k = tan=         代入**式得

              |AB| = ………… 8分

              当=时，直线AB的方程为x = 3，此时|AB| =……………… 10分

              而当=时，|AB| ==         

综上所述       所以|AB| =

       （Ⅲ）过右焦点F且与直线AB垂直的直线交椭圆M于C，D，

              同理可得       |CD| == ……………………… 12分

              有|AB| + |CD| =+=

              因为sin2∈[0，1]，所以 当且仅当sin2=1时，|AB|+|CD|有

最小值是  ………………………… 14分