题目内容
数列{an}满足a1，a2-a1，a3-a2，…，an-an-1是首项为1，公比为2的等比数列，那么an=（ ）A．2n-1
B．2n-1-1
C．2n+1
D．4n-1
【答案】分析：an是等比数列{an-an-1}的前n项和，利用等比数列的前n项公式可得an．
解答：解：an=（an-an-1）+（an-1-an-2）+…+（a2-a1）+a1=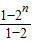
=2n-1
故选A．
点评：本题关键在于观察出所给等比数列，与an有什么关系，观察出来，此题迎刃而解．
解答：解：an=（an-an-1）+（an-1-an-2）+…+（a2-a1）+a1=
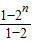=2n-1故选A．
点评：本题关键在于观察出所给等比数列，与an有什么关系，观察出来，此题迎刃而解．
练习册系列答案
相关题目