Question

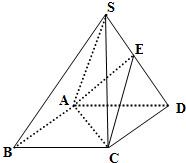如图，四棱锥S-ABCD的底面是正方形，每条侧棱的长都等于底面的边长．
（1）求证：AC⊥SD；
（2）E是侧棱SD的中点，求SB与CE所成角的正弦．

Answer 1

分析：（1）AC⊥BD，AC⊥SO?AC⊥平面SBD?AC⊥SD
（2）见中点作中位线，把异面直线SB与CE所成的角，转化为相交直线OE与CE所成的角

解答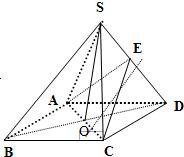：解：（1）连BD，设AC交BD于O，
∵SA=SC，∴AC⊥SO．
在正方形ABCD中，AC⊥BD，（3分）
∴AC⊥平面SBD，得AC⊥SD、（5分）
（2）∵E是AD的中点，O是BD的中点，连OE，
则OE是△DSB的中位线，
∴SB∥OE，故异面直线SB与CE所成的角为
OE与CE所成的角，即∠OEC、（8分）
设四棱维各棱长为1，则OC=

2

2

，CE=

3

2

，
又由（Ⅰ）知AC⊥平面SBD，
OE在平面SBD内，∴AC⊥OE．
∴sin∠OEC=

OC

CE

=

2

2

÷

3

2

=

6

3

．（12分）

点评：异面直线所成的角的求法：平移法，①选点，②平移，③解三角形，注意异面直线所成的角的范围是（0，

π

2

]