题目内容
设函数 .
.
①求它的定义域;②判断它的奇偶性;③求证: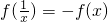 .
.
解:①由题意得:
1-x2≠0,
∴x≠±1,
∴函数的定义域为:{x|x≠±1};
②∵定义域关于原点对称,
且f(-x)= =
= =f(x),
=f(x),
∴函数是偶函数;
③∵ =-f(x),
=-f(x),
∴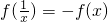 得证.
得证.
分析:①根据分母不为0,用一元二次不等式求解.
②由①知定义域关于原点对称,考查f(-x)与f(x)的关系,依据定义判断.
③先化简f( ),然后作比较发现是与-f(x)相等的式子.
),然后作比较发现是与-f(x)相等的式子.
点评:本题考查函数的定义域的求法,利用定义判断函数的奇偶性,以及利用对数的运算性质证明等式.属于基础题.
1-x2≠0,
∴x≠±1,
∴函数的定义域为:{x|x≠±1};
②∵定义域关于原点对称,
且f(-x)=
 =
= =f(x),
=f(x),∴函数是偶函数;
③∵
 =-f(x),
=-f(x),∴
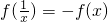 得证.
得证.分析:①根据分母不为0,用一元二次不等式求解.
②由①知定义域关于原点对称,考查f(-x)与f(x)的关系,依据定义判断.
③先化简f(
 ),然后作比较发现是与-f(x)相等的式子.
),然后作比较发现是与-f(x)相等的式子.点评:本题考查函数的定义域的求法,利用定义判断函数的奇偶性,以及利用对数的运算性质证明等式.属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目