题目内容
在棱长为 的正方体ABCD-A1B1C1D1中,正方形BCC1B1所在平面内的动点P到直线D1C1、DC的距离之和为4,则
的正方体ABCD-A1B1C1D1中,正方形BCC1B1所在平面内的动点P到直线D1C1、DC的距离之和为4,则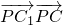 的取值范围是________.
的取值范围是________.
[-2, ]
]
分析:先将在面BCC1B1内动点P到直线D1C1、DC的距离转化为P到点C1,C的距离,从而动点P到直线C1、C的距离之和为4,由椭圆的定义即知P点的轨迹是一个椭圆.建立适当的直角坐标系,即可求出点P的轨迹方程;根据向量的坐标运算求出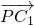 ,
, 的坐标,再代入
的坐标,再代入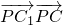 整理为关于x的函数,结合x的取值范围即可求出
整理为关于x的函数,结合x的取值范围即可求出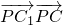 的取值范围.
的取值范围.
解答: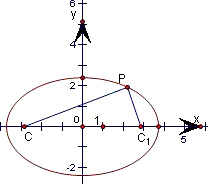 解:在面BCC1B1内到直线D1C1、DC的距离即为P到点C1,C的距离,
解:在面BCC1B1内到直线D1C1、DC的距离即为P到点C1,C的距离,
故有面BCC1B1内的点P到直线C1、C的距离之和为4,
由椭圆的定义即知点的轨迹是椭圆的一部分.
以CC1所在的直线为x轴,线段CC1的中心为坐标原点,建立直角坐标系,
则C(- ,0),C1(
,0),C1( ,0),
,0),
∴c= ,a=2,b=1.
,a=2,b=1.
设P(x,y),得椭圆的方程为: .
.
∴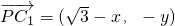 ,
,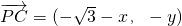
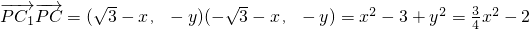
由P在正方形BCC1B1所在平面内,
∴x∈[- ,
, ],
],
故有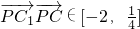 .
.
故答案为:[-2, ].
].
点评:本题主要考查了椭圆的定义及空间中距离的相互转化,解答的易错点是不会将空间中距离转化为一个平面上的距离,从而不会应用椭圆的定义.本题还主要考查平面向量数量积的运算,考查了运算能力.
 ]
]分析:先将在面BCC1B1内动点P到直线D1C1、DC的距离转化为P到点C1,C的距离,从而动点P到直线C1、C的距离之和为4,由椭圆的定义即知P点的轨迹是一个椭圆.建立适当的直角坐标系,即可求出点P的轨迹方程;根据向量的坐标运算求出
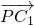 ,
, 的坐标,再代入
的坐标,再代入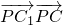 整理为关于x的函数,结合x的取值范围即可求出
整理为关于x的函数,结合x的取值范围即可求出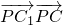 的取值范围.
的取值范围.解答:
 解:在面BCC1B1内到直线D1C1、DC的距离即为P到点C1,C的距离,
解:在面BCC1B1内到直线D1C1、DC的距离即为P到点C1,C的距离,故有面BCC1B1内的点P到直线C1、C的距离之和为4,
由椭圆的定义即知点的轨迹是椭圆的一部分.
以CC1所在的直线为x轴,线段CC1的中心为坐标原点,建立直角坐标系,
则C(-
 ,0),C1(
,0),C1( ,0),
,0),∴c=
 ,a=2,b=1.
,a=2,b=1.设P(x,y),得椭圆的方程为:
 .
.∴
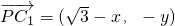 ,
,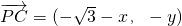
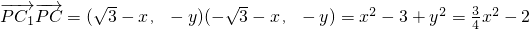
由P在正方形BCC1B1所在平面内,
∴x∈[-
 ,
, ],
],故有
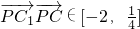 .
.故答案为:[-2,
 ].
].点评:本题主要考查了椭圆的定义及空间中距离的相互转化,解答的易错点是不会将空间中距离转化为一个平面上的距离,从而不会应用椭圆的定义.本题还主要考查平面向量数量积的运算,考查了运算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
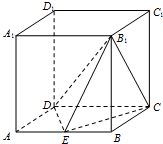 如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为AB的中点.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为AB的中点.