题目内容
设0<a<1,集合A={x∈R|x>0},B={x∈R|2x2-3(1+a)x+6a>0},D=A∩B。
(1)求集合D(用区间表示)
(2)求函数f(x)=2x3-3(1+a)x2+6ax在D内的极值点。
(1)求集合D(用区间表示)
(2)求函数f(x)=2x3-3(1+a)x2+6ax在D内的极值点。
解:(1)对于方程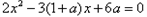 判别式
判别式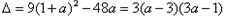
因为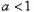 ,
,
所以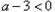
①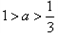 时,
时,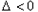 ,此时
,此时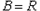 ,
,
所以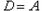 ;
;
②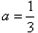 时,
时,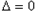 ,此时
,此时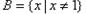 ,
,
所以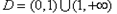 ;
;
当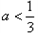 时,
时,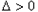 ,
,
设方程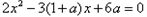 的两根为
的两根为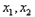 且
且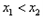 ,
,
则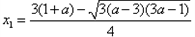 ,
,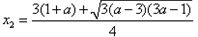
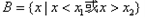
③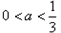 时,
时,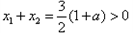 ,
,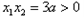 ,
,
所以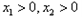
此时,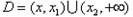
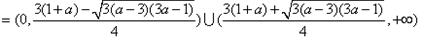 ;
;
(2)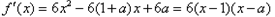 ,
,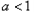
所以函数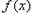 在区间
在区间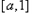 上为减函数,在区间
上为减函数,在区间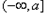 和
和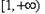 上为增函数
上为增函数
①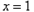 是极点
是极点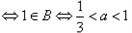
②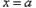 是极点
是极点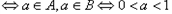
得: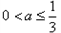 时,
时,
函数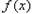 极值点为
极值点为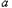 ,
,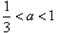 时,函数
时,函数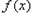 极值点为
极值点为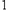 与
与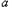 。
。
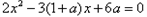 判别式
判别式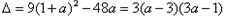
因为
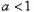 ,
,所以
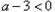
①
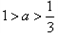 时,
时,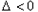 ,此时
,此时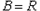 ,
,所以
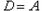 ;
;②
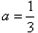 时,
时,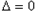 ,此时
,此时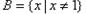 ,
,所以
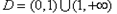 ;
;当
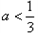 时,
时,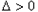 ,
,设方程
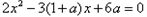 的两根为
的两根为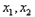 且
且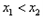 ,
,则
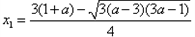 ,
,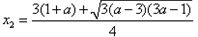
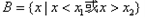
③
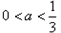 时,
时,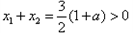 ,
,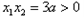 ,
,所以
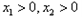
此时,
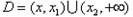
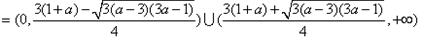 ;
;(2)
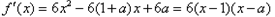 ,
,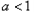
所以函数
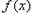 在区间
在区间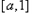 上为减函数,在区间
上为减函数,在区间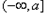 和
和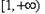 上为增函数
上为增函数 ①
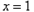 是极点
是极点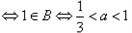
②
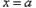 是极点
是极点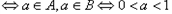
得:
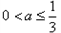 时,
时,函数
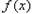 极值点为
极值点为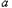 ,
,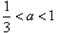 时,函数
时,函数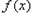 极值点为
极值点为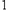 与
与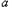 。
。
练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目