题目内容
如图所示,在棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,且AB∥CD,∠BAD=90°,PA=AD=DC=2,AB=4.(Ⅰ)求证:BC⊥PC;
(Ⅱ)求PB与平面PAC所成角的正弦值.
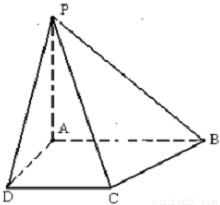
【答案】分析:(Ⅰ)取AB中点E,连接CE,根据题意可得:AE=CE=2,得到△ABC为等腰直角三角形,所以AC⊥BC,又PA⊥BC,再结合线面垂直的判定定理可得线面垂直,进而得到线线垂直.
(Ⅱ)以A为坐标原点,AD,AB,AP分别为x,y,z轴,建立如图所示的坐标系,求出直线所在的向量与平面的法向量,再求出两个向量的夹角,进而转化为线面角.
解答: 解:(Ⅰ)在直角梯形ABCD中,AC=
解:(Ⅰ)在直角梯形ABCD中,AC= ,
,
取AB中点E,连接CE,
则四边形AECD为正方形,…(2分)
∴AE=CE=2,
又BE= ,
,
所以△ABC为等腰直角三角形,
∴AC⊥BC,…(4分)
又∵PA⊥平面ABCD,BC?平面ABCD,
∴PA⊥BC,由AC∩PA=A,
所以BC⊥平面PAC,
∵PC?平面PAC,
所以BC⊥PC.…(6分)
(Ⅱ)以A为坐标原点,AD,AB,AP分别为x,y,z轴,建立如图所示的坐标系.
则P(0,0,2),B(0,4,0),C(2,2,0),
所以 .…(9分)
.…(9分)
由(Ⅰ)知 即为平面PAC的一个法向量,
即为平面PAC的一个法向量, ,…(11分)
,…(11分)
即PB与平面PAC所成角的正弦值为 .…(12分)
.…(12分)
点评:解决此类问题的关键是熟练掌握几何体的结构特征,进而得到空间中点、线、面的位置关系,结合有关定理进行证明即可,并且也有利于建立空间之间坐标系,利用向量的有关知识解决空间角与空间距离等问题.
(Ⅱ)以A为坐标原点,AD,AB,AP分别为x,y,z轴,建立如图所示的坐标系,求出直线所在的向量与平面的法向量,再求出两个向量的夹角,进而转化为线面角.
解答:
 解:(Ⅰ)在直角梯形ABCD中,AC=
解:(Ⅰ)在直角梯形ABCD中,AC= ,
,取AB中点E,连接CE,
则四边形AECD为正方形,…(2分)
∴AE=CE=2,
又BE=
 ,
,所以△ABC为等腰直角三角形,
∴AC⊥BC,…(4分)
又∵PA⊥平面ABCD,BC?平面ABCD,
∴PA⊥BC,由AC∩PA=A,
所以BC⊥平面PAC,
∵PC?平面PAC,
所以BC⊥PC.…(6分)
(Ⅱ)以A为坐标原点,AD,AB,AP分别为x,y,z轴,建立如图所示的坐标系.
则P(0,0,2),B(0,4,0),C(2,2,0),
所以
 .…(9分)
.…(9分)由(Ⅰ)知
 即为平面PAC的一个法向量,
即为平面PAC的一个法向量, ,…(11分)
,…(11分)即PB与平面PAC所成角的正弦值为
 .…(12分)
.…(12分)点评:解决此类问题的关键是熟练掌握几何体的结构特征,进而得到空间中点、线、面的位置关系,结合有关定理进行证明即可,并且也有利于建立空间之间坐标系,利用向量的有关知识解决空间角与空间距离等问题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
 如图所示,在棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,PA=AD=DC=2,AB=4且AB∥CD,∠BAD=90°
如图所示,在棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,PA=AD=DC=2,AB=4且AB∥CD,∠BAD=90°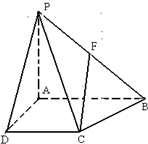 如图所示,在棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,且AB∥CD,∠BAD=90°,PA=AD=DC=2,AB=4.
如图所示,在棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,且AB∥CD,∠BAD=90°,PA=AD=DC=2,AB=4. 如图所示,在棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,且AB∥CD,∠BAD=90°,PA=AD=DC=2,AB=4.
如图所示,在棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,且AB∥CD,∠BAD=90°,PA=AD=DC=2,AB=4. 如图所示,在棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,且AB∥CD,∠BAD=90°,PA=AD=DC=2,AB=4.
如图所示,在棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,且AB∥CD,∠BAD=90°,PA=AD=DC=2,AB=4.