题目内容
自极点O作射线与直线ρcosθ=3相交于点M,在OM上取一点P,使得OM•OP=12,求点P的轨迹方程,并判断点P的轨迹与直线l:
|
分析:先利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,将直线ρcosθ=3化成直角坐标方程,消去参数后将直线l:
(t是参数)化成直角坐标方程,再利用直角坐标求解即可.
|
解答:C、解:P(ρ,θ),则M(ρ',θ),因为OM•OP=12,所以ρρ'=12,
又ρ'cosθ=3,所以ρ
=12,
即点P的轨迹方程为ρ=4cosθ,(5分)
化为直角坐标方程为(x-2)2+y2=4,直线l的普通方程为:2x-y-3=0,
则圆心(2,0)到直线l的距离为:d=
=
<2,
所以直线l与点P的轨迹相交.(10分)
又ρ'cosθ=3,所以ρ
| 3 |
| cosθ |
即点P的轨迹方程为ρ=4cosθ,(5分)
化为直角坐标方程为(x-2)2+y2=4,直线l的普通方程为:2x-y-3=0,
则圆心(2,0)到直线l的距离为:d=
| |4-3| | ||
|
| ||
| 5 |
所以直线l与点P的轨迹相交.(10分)
点评:本题考查点的极坐标和直角坐标的互化,能在极坐标系中用极坐标刻画点的位置,体会在极坐标系和平面直角坐标系中刻画点的位置的区别,能进行极坐标和直角坐标的互化.

练习册系列答案
相关题目
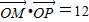 ,求点P的轨迹的极坐标方程.
,求点P的轨迹的极坐标方程.