题目内容
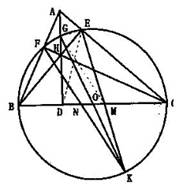
如图,AD,BE,CF分别是锐角△ABC的三条高,垂足分别为D,E,F,以BC为为直径的圆O和AD交于G点,过G的直径的另一端点为K,若EK,FK和BC分别交于M,N。求证:OM=ON。
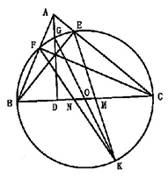
证明:AD,BE,CF分别是锐角△ABC的三条高
∴它们必相交于一点,记为H
∴H为△ABC的垂心 (5分)
连结GE,GM,DE
∵GK是⊙O的直径 ∴∠GEM = 90°
∵∠GDM = 90° ∴G,D,M,E四点共圆 (10分)
∴∠GME = ∠GDE
又∵H,D,C,E四点共圆,∴∠GDE = ∠HDE = ∠HCE
∴∠GME = ∠HCE = ∠FKE, ∴GM∥FK (5分)
∴∠OMG = ∠ONK,
∵∠GOM = ∠KON, GO = KO,
∴△OMG≌△ONK,∴OM = ON (20分)

练习册系列答案
相关题目
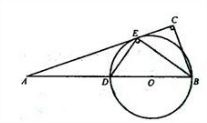 如图,在△ABC中,∠C=90°,BE是角平分线,DE⊥BE交AB于D,⊙O是△BDE的外接圆.
如图,在△ABC中,∠C=90°,BE是角平分线,DE⊥BE交AB于D,⊙O是△BDE的外接圆.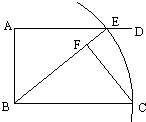 (选修4-1几何证明选讲)
(选修4-1几何证明选讲) 选修4-1:几何证明选讲
选修4-1:几何证明选讲
 ,求BC的长.
,求BC的长.