题目内容
sin6°•cos24°•sin78°•cos48°的值为( )
A、
| ||
B、-
| ||
C、
| ||
D、
|
分析:把原式的第三项利用诱导公式把正弦化简为余弦后,给原式的分子分母都乘以24cos6°,然后分子连续利用四次二倍角的正弦函数公式后再利用诱导公式把正弦化为余弦,约分即可得到值.
解答:解:sin6°•cos24°•sin78°•cos48°
=sin6°•sin(90°-12°)•cos24°•cos48°
=sin6°cos12°cos24°cos48°
=
=
=
=
=
=
=
=
.
故选A
=sin6°•sin(90°-12°)•cos24°•cos48°
=sin6°cos12°cos24°cos48°
=
| 24cos6°sin6°cos12°cos24°cos48° |
| 24cos6° |
=
| 23sin12°cos12°cos24°cos48° |
| 24cos6° |
=
| 22sin24°cos24°cos48° |
| 24cos6° |
=
| 2 sin48°cos48° |
| 24cos6° |
| sin96° |
| 24cos6° |
| sin(90°+6°) |
| 16cos6° |
| cos6° |
| 16cos6° |
| 1 |
| 16 |
故选A
点评:本题考查l诱导公式及二倍角的正弦函数公式,是一道中档题.此题的突破点是分子变形后给分子分母都乘以16cos6°以至于造成了一系列的连锁反应.

练习册系列答案
相关题目
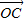 =cosθ
=cosθ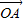 +cos2θ
+cos2θ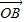 ,则sin2θ+sin4θ+sin6θ=( )
,则sin2θ+sin4θ+sin6θ=( )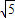
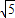
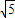 或1+
或1+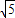
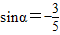 ,且α为第三象限角,求cosα,cos2α的值
,且α为第三象限角,求cosα,cos2α的值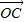 =cosθ
=cosθ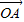 +cos2θ
+cos2θ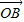 ,则sin2θ+sin4θ+sin6θ=( )
,则sin2θ+sin4θ+sin6θ=( )
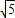
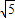 或1+
或1+