题目内容
16．1202年，意大利数学家斐波那契在他的书中给出了一个关于兔子繁殖的递推关系：${F}_{n}{=}_{{F}_{n-1}}{+}_{{F}_{n-2}}$（n≥3），其中Fn表示第n个月的兔子的总对数，F1=F2=1，则F8的值为（ ）| A． | 13 | B． | 21 | C． | 34 | D． | 55 |
分析 直接由已知计算得答案．
解答 解：由${F}_{n}{=}_{{F}_{n-1}}{+}_{{F}_{n-2}}$（n≥3），且F1=F2=1，
则F3=F2+F1=2，F4=F3+F2=3，
F5=F4+F3=5，F6=F5+F4=8，F7=F6+F5=13，F8=F7+F6=21．
故选：B．
点评 本题考查数列递推式，是基础的计算题．
练习册系列答案
阅读快车系列答案
相关题目
如图，点A的坐标为（1，0），点C的坐标为（2，4），函数f（x）=x2，利用随机模拟方法计算阴影部分面积时，利用计算器产生两组0～1之间的均匀随机数a1=RAND，b1=RAND，然后进行平移与伸缩变换a=a1+1，b=4b1，试验进行100次，前98次中落在阴影部分内的样本点数为40，且最后两次试验的随机数为a1=0.5，b1=0.3及a1=0.2，b1=0.6，那么本次模拟得出的面积约为1.64．
5．己知随机变量X服从正态分布N（μ，σ2），且P（μ-2σ＜X≤μ+2σ）=0.9545，P（μ-σ＜X≤μ+σ）=0.6827，若μ=3，σ=1，则P（4＜X≤5）=（ ）
| A． | 0.1358 | B． | 0.1359 | C． | 0.2716 | D． | 0.2718 |
6．
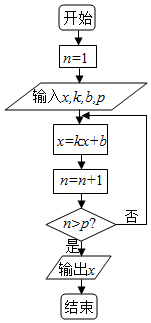如图所示的程序框图，若输入x，k，b，p的值分别为1，-2，9，3，则输出x的值为（ ）
如图所示的程序框图，若输入x，k，b，p的值分别为1，-2，9，3，则输出x的值为（ ）| A． | -29 | B． | 19 | C． | 47 | D． | -5 |