题目内容
已知数列{ an}、{ bn}满足: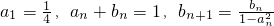 .
.
(1)求a2,a3,;
(2)证数列{ }为等差数列,并求数列{an}和{ bn}的通项公式;
}为等差数列,并求数列{an}和{ bn}的通项公式;
(3)设Sn=a1a2+a2a3+a3a4+…+anan+1,求实数λ为何值时4λSn<bn恒成立.
(1)解:∵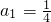 ,∴
,∴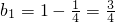 ,
,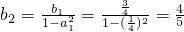 ,
,
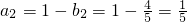 ,
,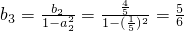 ,
,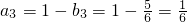 .
.
∴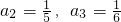 ;
;
(2)证明:由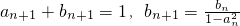 ,
,
∴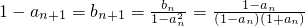 =
= ,
,
∴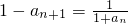 ,即an-an+1=anan+1,
,即an-an+1=anan+1,
∴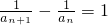
∴数列{ }是以4为首项,1为公差的等差数列.
}是以4为首项,1为公差的等差数列.
∴ ,则
,则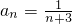 ,
,
∴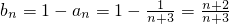 ;
;
(3)解:由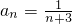 ,
,
∴Sn=a1a2+a2a3+…+anan+1
=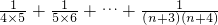
=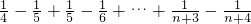
=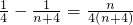 .
.
∴ ,
,
要使4λSn<bn恒成立,只需(λ-1)n2+(3λ-6)n-8<0恒成立,
设f(n)=(λ-1)n2+3(λ-2)n-8
当λ=1时,f(n)=-3n-8<0恒成立,
当λ>1时,由二次函数的性质知f(n)不满足对于任意n∈N*恒成立,
当λ<l时,对称轴n=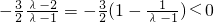
f(n)在[1,+∞)为单调递减函数.
只需f(1)=(λ-1)n2+(3λ-6)n-8=(λ-1)+(3λ-6)-8=4λ-15<0
∴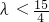 ,∴λ≤1时4λSn<bn恒成立.
,∴λ≤1时4λSn<bn恒成立.
综上知:λ≤1时,4λSn<bn恒成立.
分析:(1)由给出的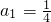 ,循环代入an+bn=1和
,循环代入an+bn=1和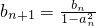 可求解a2,a3;
可求解a2,a3;
(2)由an+bn=1得an+1+bn+1=1,结合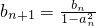 ,去掉bn与bn+1得到an+1与an的关系式,整理变形后可证得数列{
,去掉bn与bn+1得到an+1与an的关系式,整理变形后可证得数列{ }是以4为首项,1为公差的等差数列,求出其通项公式后即可求得数列{an}和{ bn}的通项公式;
}是以4为首项,1为公差的等差数列,求出其通项公式后即可求得数列{an}和{ bn}的通项公式;
(3)首先利用裂项求和求出Sn,代入4λSn<bn,通过对λ分类讨论,结合二次函数的最值求使4λSn<bn恒成立的实数λ的值.
点评:本题考查了等差、等比数列的通项公式,考查了数列的裂项求和,考查了数列的函数特性,训练了恒成立问题的求解方法,解答过程中注意分类讨论的数学思想,属中档题.
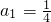 ,∴
,∴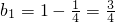 ,
,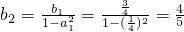 ,
,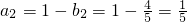 ,
,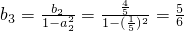 ,
,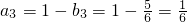 .
.∴
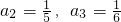 ;
;(2)证明:由
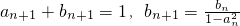 ,
,∴
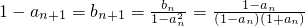 =
= ,
,∴
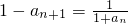 ,即an-an+1=anan+1,
,即an-an+1=anan+1,∴
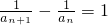
∴数列{
 }是以4为首项,1为公差的等差数列.
}是以4为首项,1为公差的等差数列.∴
 ,则
,则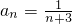 ,
,∴
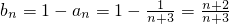 ;
;(3)解:由
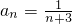 ,
,∴Sn=a1a2+a2a3+…+anan+1
=
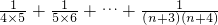
=
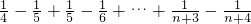
=
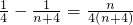 .
.∴
 ,
,要使4λSn<bn恒成立,只需(λ-1)n2+(3λ-6)n-8<0恒成立,
设f(n)=(λ-1)n2+3(λ-2)n-8
当λ=1时,f(n)=-3n-8<0恒成立,
当λ>1时,由二次函数的性质知f(n)不满足对于任意n∈N*恒成立,
当λ<l时,对称轴n=
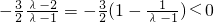
f(n)在[1,+∞)为单调递减函数.
只需f(1)=(λ-1)n2+(3λ-6)n-8=(λ-1)+(3λ-6)-8=4λ-15<0
∴
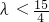 ,∴λ≤1时4λSn<bn恒成立.
,∴λ≤1时4λSn<bn恒成立.综上知:λ≤1时,4λSn<bn恒成立.
分析:(1)由给出的
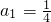 ,循环代入an+bn=1和
,循环代入an+bn=1和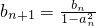 可求解a2,a3;
可求解a2,a3;(2)由an+bn=1得an+1+bn+1=1,结合
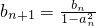 ,去掉bn与bn+1得到an+1与an的关系式,整理变形后可证得数列{
,去掉bn与bn+1得到an+1与an的关系式,整理变形后可证得数列{ }是以4为首项,1为公差的等差数列,求出其通项公式后即可求得数列{an}和{ bn}的通项公式;
}是以4为首项,1为公差的等差数列,求出其通项公式后即可求得数列{an}和{ bn}的通项公式;(3)首先利用裂项求和求出Sn,代入4λSn<bn,通过对λ分类讨论,结合二次函数的最值求使4λSn<bn恒成立的实数λ的值.
点评:本题考查了等差、等比数列的通项公式,考查了数列的裂项求和,考查了数列的函数特性,训练了恒成立问题的求解方法,解答过程中注意分类讨论的数学思想,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目