题目内容
已知函数 ,求
,求
(1)函数的最小值及此时的 的集合.
的集合.
(2)函数的单调减区间.
(1)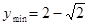 ,此时
,此时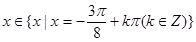 ;(2)
;(2)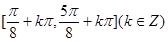
解析试题分析:(1)先由三角恒等变换化简得函数解析式为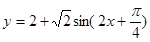 ,然后由三角函数的性质由
,然后由三角函数的性质由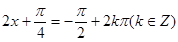 时可求
时可求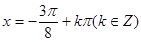 时
时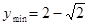 ;
;
(2)由三角函数的单调性可得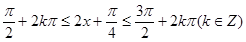 求得单调减区间为
求得单调减区间为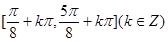 .
.
试题解析:(1)由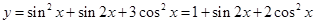
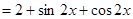
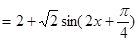 ,
,
故当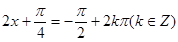 即
即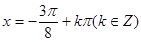 时
时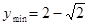 ,
,
此时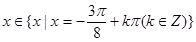
由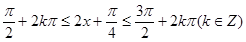 解得
解得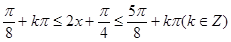 ,
,
即所求的单调减区间为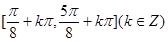 .
.
考点:1.三角函数的性质;2.三角恒等变换

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
题目内容
已知函数 ,求
,求
(1)函数的最小值及此时的 的集合.
的集合.
(2)函数的单调减区间.
(1)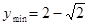 ,此时
,此时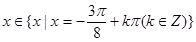 ;(2)
;(2)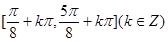
解析试题分析:(1)先由三角恒等变换化简得函数解析式为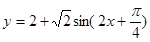 ,然后由三角函数的性质由
,然后由三角函数的性质由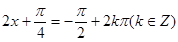 时可求
时可求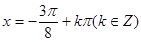 时
时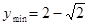 ;
;
(2)由三角函数的单调性可得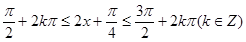 求得单调减区间为
求得单调减区间为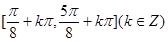 .
.
试题解析:(1)由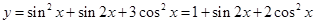
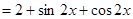
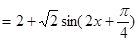 ,
,
故当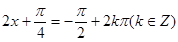 即
即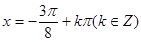 时
时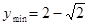 ,
,
此时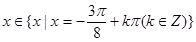
由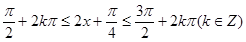 解得
解得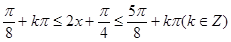 ,
,
即所求的单调减区间为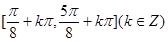 .
.
考点:1.三角函数的性质;2.三角恒等变换

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案