题目内容
3.若a,b,c∈R+,求证:(a+b+c)(a3+b3+c3)≥(a2+b2+c2)2.分析 运用作差法,注意运用乘法公式,化简整理,即可得证.
解答 证明:由(a+b+c)(a3+b3+c3)-(a2+b2+c2)2
=a4+ab3+ac3+ba3+b4+bc3+ca3+cb3+c4-(a4+b4+c4+2a2b2+2a2c2+2b2c2)
=(ab3-2a2b2+ba3)+(bc3-2b2c2+cb3)+(ac3-2a2c2+ca3)
=ab(b2-2ab+a2)+bc(c2-2bc+b2)+ac(c2-2ac+a2)
=ab(a-b)2+bc(b-c)2+ca(c-a)2≥0,
则有(a+b+c)(a3+b3+c3)≥(a2+b2+c2)2.
点评 本题考查不等式的证明,注意运用作差比较法,考查运算能力,属于中档题.

练习册系列答案
相关题目
11.设P是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)上一点,F1(-c,0),F2(c,0)(c>0)为左、右焦点,△PF1F2周长为6c,面积为$\frac{2\sqrt{3}}{3}$a2,则双曲线的离心率是( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | 3 |
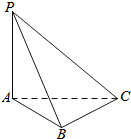 如图所示,PA⊥平面ABC,AC⊥BC,AB=2,BC=$\sqrt{2}$,PB=$\sqrt{6}$,则二面角P-BC-A的大小为45°.
如图所示,PA⊥平面ABC,AC⊥BC,AB=2,BC=$\sqrt{2}$,PB=$\sqrt{6}$,则二面角P-BC-A的大小为45°.