Question

在△ABC中，已知内角A，B，C所对的边分别为a，b，c，向量，，且∥．
（1）求锐角B的大小；
（2）设，且B为钝角，求ac的最大值．

Answer 1

解：（1）由∥，
得

解法一：即

∵，
∴，
∴，
即锐角

解法二：即．
即

又∵B为锐角，
∴2B∈（0，π）．
∴，
∴

（2）∵B为钝角，由（Ⅰ）知：，b=，
∴由余弦定理得：
得：，
∴，
∴ac的最大值为：．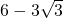

分析：（1）由∥得．法一：，所以，由此能求出∠B．法二：．所以．由此能求出∠B．
（2）由B为钝角，知，b=，由余弦定理得：，由此能求出ac的最大值．
点评：本题考查平面向量的应用，解题时要认真审题，注意三角函数的恒等式和余弦定理的灵活运用．