题目内容
求下列函数的定义域和值域
(I)y=x-2;
(II)f(x)=log ;
;
(III)y=( )x+(
)x+( )x+1.
)x+1.
解:(I)
∴函数的定义域为(-∞,0)∪(0,+∞);值域为(0,+∞);
(II)f(x)=log 的定义域为R;
的定义域为R;
∵3x>0,∴3x+1>1
∴log >0
>0
∴函数的值域为(0,+∞);
(III)y=( )x+(
)x+( )x+1的定义域为R;
)x+1的定义域为R;
设t=( )x,则t>0,y=t2+t+1=
)x,则t>0,y=t2+t+1=
∵t>0,∴ 在
在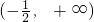 单调递增
单调递增
∴y>1
∴函数的值域为(1,+∞).
分析:(I)利用分母不为0,可得函数的定义域,从而可得函数的值域;
(II)f(x)=log 的定义域为R,利用指数、对数函数的性质,可得结论;
的定义域为R,利用指数、对数函数的性质,可得结论;
(III)y=( )x+(
)x+( )x+1的定义域为R;换元,利用二次函数的单调性,即可得出结论.
)x+1的定义域为R;换元,利用二次函数的单调性,即可得出结论.
点评:本题考查函数的定义域和值域,考查学生分析解决问题的能力,属于中档题.

∴函数的定义域为(-∞,0)∪(0,+∞);值域为(0,+∞);
(II)f(x)=log
 的定义域为R;
的定义域为R;∵3x>0,∴3x+1>1
∴log
 >0
>0∴函数的值域为(0,+∞);
(III)y=(
 )x+(
)x+( )x+1的定义域为R;
)x+1的定义域为R;设t=(
 )x,则t>0,y=t2+t+1=
)x,则t>0,y=t2+t+1=
∵t>0,∴
 在
在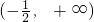 单调递增
单调递增∴y>1
∴函数的值域为(1,+∞).
分析:(I)利用分母不为0,可得函数的定义域,从而可得函数的值域;
(II)f(x)=log
 的定义域为R,利用指数、对数函数的性质,可得结论;
的定义域为R,利用指数、对数函数的性质,可得结论;(III)y=(
 )x+(
)x+( )x+1的定义域为R;换元,利用二次函数的单调性,即可得出结论.
)x+1的定义域为R;换元,利用二次函数的单调性,即可得出结论.点评:本题考查函数的定义域和值域,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目