题目内容

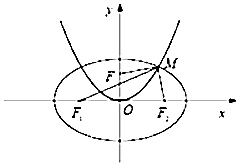
【题目】在平面直角坐标系xOy中，已知椭圆 + =1（a＞b＞0）与双曲线 ﹣y2=1有相同的焦点F1 ， F2 ， 抛物线x2=2py（p＞0）的焦点为F，且与椭圆在第一象限的交点为M，若|MF1|+|MF2|=2 ．

（1）求椭圆的方程；
（2）若|MF|= ，求抛物线的方程．

【答案】
（1）解：由条件得 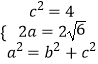，解得a= ，b= ，

∴椭圆方程为 =1


（2）解：设M（x0，y0），则|MF|=y0+ = ，即p= ﹣2y0，

又M在椭圆上，

∴x02+3y02=6，且x02=2py0，

∴（7﹣4y0）y0+3y02=6，解得y0=1或y0=6（舍），

∴p= ，

∴抛物线方程为x2=3y


【解析】（1）根据椭圆定义可知|MF1|+|MF2|=2a；（2）根据抛物线x2=2py（p0）上的点（x0，y0）到焦点的距离d=y0+将y0用p表示，然后将（x0，y0）分别代入椭圆方程及抛物线方程，联立组成方程组.

练习册系列答案
相关题目

【题目】函数f（x）=x2+bx﹣1（b∈R）．
（1）若函数y=f（x）在[1，+∞）上单调，求b的取值范围；
（2）若函数y=|f（x）|﹣2有四个零点，求b的取值范围；
（3）若函数y=|f（x）|在[0，|b|）上的最大值为g（b），求g（b）的表达式．

【题目】已知函数f（x）=lnx+ ，其中a为大于零的常数．．
（1）若函数f（x）在区间[1，+∞）内单调递增，求a的取值范围；
（2）求函数f（x）在区间[1，2]上的最小值；
（3）求证：对于任意的n∈N* ， 且n＞1时，都有lnn＞ + +…+ 成立．

【题目】已知平行四边形ABCD的三个顶点的坐标为A（﹣1，5），B（﹣2，﹣1），C（2，3）．

（1）求平行四边形ABCD的顶点D的坐标；
（2）在△ACD中，求CD边上的高所在直线方程；
（3）求四边形ABCD的面积．

【题目】已知数列{an}中，a1=1，a2=4，a3=10，若{an+1﹣an}是等比数列，则 i= ．

【题目】某校高一（1）班全体男生的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，但可见部分如图所示，据此解答如下问题：

（1）求该班全体男生的人数；

（2）求分数在之间的男生人数，并计算频率公布直方图中之间的矩形的高；

【题目】已知点O为△ABC的外心，角A，B，C的对边分别满足a，b，c， （Ⅰ）若3 +4 +5 = ，求cos∠BOC的值；
（Ⅱ）若 = ，求 的值．

【题目】在平面直角坐标系中，已知圆的方程是．

（）如果圆与直线没有公共点，求实数的取值范围；

（）如果圆过坐标原点，过点直线与圆交于， 两点，记直线的斜率的平方为，对于每一个确定的，当的面积最大时，用含的代数式表示，并求的最大值．

【题目】若点O和点F2（﹣ ，0）分别为双曲线 =1（a＞0）的中心和左焦点，点P为双曲线右支上的任意一点，则 的取值范围为 ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网