题目内容
设关于 的一元二次方程
的一元二次方程 .
.
(1)若 是从
是从 、
、 、
、 、
、 四个数中任取的一个数,
四个数中任取的一个数, 是从
是从 、
、 、
、 三个数中任取的一个数,求上述方程有实根的概率;
三个数中任取的一个数,求上述方程有实根的概率;
(2)若 是从区间
是从区间 任取的一个数,
任取的一个数, 是从区间
是从区间 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.
【答案】
(1)上述方程有实根的概率为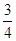 ;(2)上述方程有实根的概率为
;(2)上述方程有实根的概率为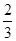 .
.
【解析】
试题分析:(1)先将全部的基本事件以及问题中涉及事件所包含的基本事件列举出来,确定基本事件总数与问题中涉及事件所包含的基本事件的数目,然后利用古典概型的概率计算公式计算出相应事件的概率;(2)先利用方程有根这一条件转化为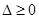 ,从而确定
,从而确定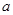 、
、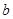 所满足的条件,然后综合
所满足的条件,然后综合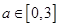 ,
,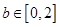 这些条件,将问题量化为平面区域的面积比的几何概型的概率来进行处理.
这些条件,将问题量化为平面区域的面积比的几何概型的概率来进行处理.
试题解析:设事件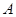 为“方程
为“方程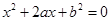 有实根”,
有实根”,
当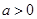 ,
,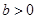 时,方程
时,方程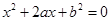 有实根的充要条件为
有实根的充要条件为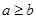 .
.
(1)基本事件共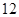 个:
个:
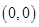 、
、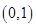 、
、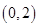 、
、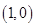 、
、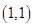 、
、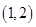 、
、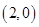 、
、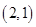 、
、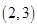 、
、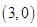 、
、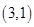 、
、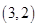 ,
,
其中第一个数表示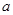 的取值,第二个数表示
的取值,第二个数表示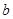 的取值.
的取值.
事件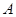 中包含
中包含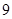 个基本事件,
个基本事件,
事件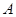 发生的概率为
发生的概率为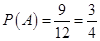 ;
;
(2)试验的全部结束所构成的区域为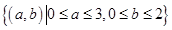 ,
,
构成事件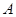 的区域为
的区域为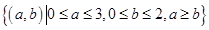 ,
,
所以所求的概率为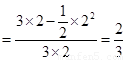 .
.
考点:古典概型与几何概型

练习册系列答案
相关题目
 的一元二次方程
的一元二次方程




 (
( )有两根
)有两根 和
和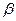 且满足
且满足 .①试用
.①试用 ;②求证:数列
;②求证:数列 是等比数列.
是等比数列.  时,求数列
时,求数列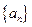 的通项公式.
的通项公式. 的一元二次方程
的一元二次方程 ,若
,若 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数, 是从0,1,2三个数中任取的一个数,求上述方程有实数根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有实数根的概率;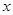 的一元二次方程
的一元二次方程 .
. ,
, 都是从集合
都是从集合 中任取的数字,求方程有实根的概率;
中任取的数字,求方程有实根的概率; 的一元二次方程
的一元二次方程 ,若
,若 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数, 是从0,1,2三个数中任取的一个数,求上述方程有实数根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有实数根的概率;