题目内容
【题目】在直角坐标系![]() 中,曲线C的参数方程为
中,曲线C的参数方程为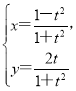 (t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线
(t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求C的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)求C上的点到![]() 距离的最大值.
距离的最大值.
【答案】(1)C的普通方程为![]() .
.![]() 的直角坐标方程为
的直角坐标方程为![]() (2)3
(2)3
【解析】
(1)把曲线C的参数方程平方相加可得普通方程,把x=ρcosθ,y=ρsinθ代入ρcosθ![]() ρsinθ+4=0,可得直线l的直角坐标方程;
ρsinθ+4=0,可得直线l的直角坐标方程;
(2)设出椭圆上动点的坐标(参数形式),再由点到直线的距离公式写出距离,利用三角函数求最值.
(1)由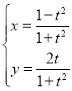 (t为参数),因为
(t为参数),因为![]() ,且
,且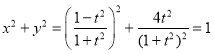 ,
,
所以C的普通方程为![]() .
.
由ρcosθ![]() ρsinθ+4=0,得x
ρsinθ+4=0,得x![]() y+4=0.
y+4=0.
即直线l的直角坐标方程为得x![]() y+4=0;
y+4=0;
(2)由(1)可设C的参数方程为![]() (
(![]() 为参数,
为参数,![]() ).
).
则P到直线得x![]() y+4=0的距离为:
y+4=0的距离为:
C上的点到![]() 的距离为
的距离为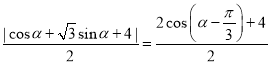 .
.
当![]() 时,
时,![]() 取得最大值6,故C上的点到
取得最大值6,故C上的点到![]() 距离的最大值为3.
距离的最大值为3.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目