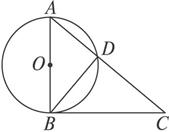
题目内容
如图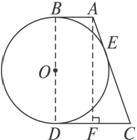
图
A.9 B
解析:连结OB,并作BO的延长线,过A作AF⊥CD,F为垂足.
∵AB切⊙O于B,∴OB⊥AB.
∵AB∥CD,∴BO⊥CD.
∴BO经过D点.∴BD为⊙O直径.
又∵AF⊥CD,
∴四边形ABDF是矩形.
在Rt△ACF中,AF=![]() .
.
由切线长定理得AB=AE,CE=CD.
∴AC=AE+CE=AB+CD=13,CF=CD-DF=CD-AB=5.
∴AF=![]() =12,OB=6.
=12,OB=6.
答案:C

练习册系列答案
相关题目
 A)选修4-1:几何证明选讲
A)选修4-1:几何证明选讲