题目内容
已知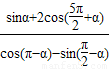
=-
．（1）求tanα的值；
（2）若β为第二象限的角，且tan（α-β）=
，求β．
【答案】分析：（1）利用诱导公式将已知条件化简成
，即可得出结果．
（2）将β写成α-（α-β），利用两角和与差正切函数公式求出tanβ=-1，进而根据β所在的象限得出结果．
解答：解：（1）∵
=
=
tanα=-
∴tanα=-
（2）∵tanβ=tan[α-（α-β）]=
=
=-1
∵β为第二象限的角
∴β=2kπ+
，k∈Z
点评：本题考查诱导公式的作用，熟练掌握公式是解题之关键，属于基础题．
，即可得出结果．（2）将β写成α-（α-β），利用两角和与差正切函数公式求出tanβ=-1，进而根据β所在的象限得出结果．
解答：解：（1）∵
==tanα=-∴tanα=-
（2）∵tanβ=tan[α-（α-β）]=
==-1∵β为第二象限的角
∴β=2kπ+
，k∈Z点评：本题考查诱导公式的作用，熟练掌握公式是解题之关键，属于基础题．
练习册系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
，（1）计算t从3秒到3.1秒内平均速度；（2）求t=3秒是瞬时速度。
，
处的切线方程；
在区间（0，1）内均存在零点。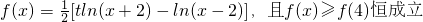
．
．