题目内容
已知双曲线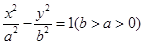 ,过右焦点
,过右焦点 作双曲线的其中一条渐近线的垂线
作双曲线的其中一条渐近线的垂线 ,垂足为
,垂足为 ,交另一条渐近线于
,交另一条渐近线于 点,若
点,若 (其中
(其中 为坐标原点),则双曲线的离心率为( )
为坐标原点),则双曲线的离心率为( )
A. | B. | C. | D. |
B
解析试题分析:由题意l的方程为ax+by-ac=0,则O点到直线的距离 ,∵
,∵ ,∴
,∴ ,又在
,又在 中,
中, ,设点Q的坐标为(m,n),则在
,设点Q的坐标为(m,n),则在 中,利用面积相等得
中,利用面积相等得 ,∴
,∴ ,联立方程
,联立方程 消x得Q的纵坐标
消x得Q的纵坐标 ,∴
,∴ ,∴
,∴ ,∴
,∴ ,∴
,∴ ,故选B
,故选B
考点:本题考查了双曲线离心率的求法
点评:解决此类问题的关键是利用题目条件找到关于a、b、c的等式关系,然后利用双曲线离心率的定义求解

练习册系列答案
相关题目
设椭圆 的左、右焦点分别为
的左、右焦点分别为 ,
, 为椭圆上异于长轴端点的一点,
为椭圆上异于长轴端点的一点, ,△
,△ 的内心为I,则
的内心为I,则 ( )
( )
A. | B. | C. | D. |
设双曲线 的虚轴长为2,焦距为
的虚轴长为2,焦距为 ,则双曲线的渐近线方程为
,则双曲线的渐近线方程为
A. | B. | C. | D. |
 ,直线l的方程为
,直线l的方程为 ,在抛物线上有一动点
,在抛物线上有一动点 到
到 轴的距离为
轴的距离为 ,到直线L的距离为
,到直线L的距离为 ,则
,则 的最小值为( )
的最小值为( )




 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,则此双曲线的离心率为( )
的焦点重合,则此双曲线的离心率为( )



 的左、右焦点分别为
的左、右焦点分别为 、
、 ,若椭圆
,若椭圆 上恰好有6个不同的点
上恰好有6个不同的点 ,使得
,使得 为等腰三角形,则椭圆
为等腰三角形,则椭圆



 分别为双曲线
分别为双曲线 的左右焦点,点P在双曲线的右支上,且
的左右焦点,点P在双曲线的右支上,且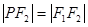 ,
, 到直线
到直线 的距离等于双曲线的实轴长,则该双曲线的离心率为( )
的距离等于双曲线的实轴长,则该双曲线的离心率为( )



 ,
, 为双曲线
为双曲线 的右焦点,点
的右焦点,点 ,
, 为
为 轴正半轴上的动点。
轴正半轴上的动点。 的最大值为( )
的最大值为( )



 的一条渐近线方程是y=
的一条渐近线方程是y= ,它的一个焦点在抛物线
,它的一个焦点在抛物线 的准线上,则双曲线的方程为
的准线上,则双曲线的方程为



