题目内容
关于x的不等式
>0的解集为P,不等式log2(x2-1)≤1的解集为Q,若Q⊆P,求正数a的取值范围.
| x-a | x+1 |
分析:解不等式log2(x2-1)≤1可得其解集Q,再解分式不等式求出其解集P,再由Q⊆P,求得正数a的取值范围.
解答:解:解不等式log2(x2-1)≤1可得0<x2-1≤2,解得1<x≤
,或-
≤x<-1.故Q={x|1<x≤
,或-
≤x<-1}.
由a>0,可得不等式
>0的解集为p={x|x<-1,或 x>a},再由Q⊆P可得 a≤1.
综合可得0<a≤1,故正数a的取值范围(0,1].
| 3 |
| 3 |
| 3 |
| 3 |
由a>0,可得不等式
| x-a |
| x+1 |
综合可得0<a≤1,故正数a的取值范围(0,1].
点评:本题主要考查分式不等式的解法,对数不等式的解法,集合关系中参数的取值范围问题,属于中档题.

练习册系列答案
相关题目
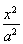




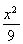




 的长半轴和短半轴.若此椭圆的一焦点与抛物线
的长半轴和短半轴.若此椭圆的一焦点与抛物线 的焦点重合,则椭圆的方程为( )
的焦点重合,则椭圆的方程为( )


