题目内容
若函数f(x)=ax•cosx在点O(0,0)处的切线与直线x-2y+3=0平行,则a=( )A.
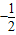
B.

C.-2
D.2
【答案】分析:由f(x)=ax•cosx,知f′(x)=acosx-axsinx,由函数f(x)=ax•cosx在点O(0,0)处的切线与直线x-2y+3=0平行,知f′(0)=acos0= ,由此能求出实数a的值.
,由此能求出实数a的值.
解答:解:∵f(x)=ax•cosx,
∴f′(x)=acosx-axsinx,
∵函数f(x)=ax•cosx在点O(0,0)处的切线与直线x-2y+3=0平行,
∴f′(0)=acos0= ,
,
∴a=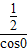 =
= .
.
故选B.
点评:本题考查利用导数求曲线上某点切线方程的斜率,解题时要认真审题,注意直线与直线平行的关系的应用.
 ,由此能求出实数a的值.
,由此能求出实数a的值.解答:解:∵f(x)=ax•cosx,
∴f′(x)=acosx-axsinx,
∵函数f(x)=ax•cosx在点O(0,0)处的切线与直线x-2y+3=0平行,
∴f′(0)=acos0=
 ,
,∴a=
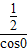 =
= .
.故选B.
点评:本题考查利用导数求曲线上某点切线方程的斜率,解题时要认真审题,注意直线与直线平行的关系的应用.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目