题目内容
在△ABC中,已知AC=2,BC=3,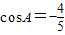 .
.(Ⅰ)求sinB的值;
(Ⅱ)求
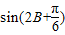 的值.
的值.
【答案】分析:(1)利用cosA,求得sinA,进而根据正弦定理求得sinB.
(2)根据cosA小于0判断A为钝角,从而角B为锐角,进而根据sinB求得cosB和cos2B,进而利用倍角公式求得sin2B,最后根据两角和公式求得答案.
解答:(Ⅰ)解:在△ABC中,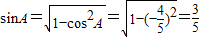 ,由正弦定理,
,由正弦定理,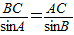 .
.
所以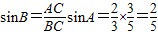 .
.
(Ⅱ)解:∵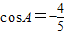 ,所以角A为钝角,从而角B为锐角,
,所以角A为钝角,从而角B为锐角,
∴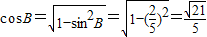 ,
,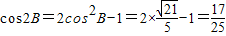 ,
,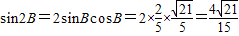 .
.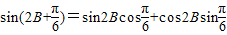 =
=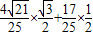 =
=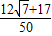 .
.
点评:本小题考查同角三角函数的基本关系式、两角和公式、倍角公式、正弦定理等的知识,考查基本运算能力
(2)根据cosA小于0判断A为钝角,从而角B为锐角,进而根据sinB求得cosB和cos2B,进而利用倍角公式求得sin2B,最后根据两角和公式求得答案.
解答:(Ⅰ)解:在△ABC中,
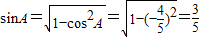 ,由正弦定理,
,由正弦定理,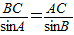 .
.所以
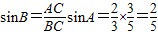 .
.(Ⅱ)解:∵
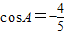 ,所以角A为钝角,从而角B为锐角,
,所以角A为钝角,从而角B为锐角,∴
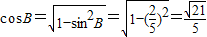 ,
,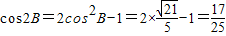 ,
,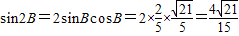 .
.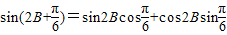 =
=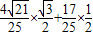 =
=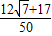 .
.点评:本小题考查同角三角函数的基本关系式、两角和公式、倍角公式、正弦定理等的知识,考查基本运算能力

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目