题目内容
设函数f(x)=x|x-a|-2.
(1)若a=-2,写出函数f(x)的单调区间;
(2)若a>0,写出函数f(x)的单调区间;
(3)若a<1,且当x∈[0,1]时,恒有f(x)<0,求a的取值范围.
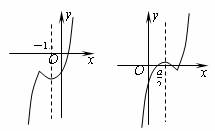
解 (1) f(x)=x|x+2|-2=![]()
=![]()
结合函数图象,单调增区间为(-∞,-2]和[-1,+∞),减区间为[-2,-1].
(2) f(x)=x|x-a|-2=![]()
=
结合函数图象,单调增区间为(-∞,![]() ]和[a,+∞),减区间为[
]和[a,+∞),减区间为[![]() ,a].
,a].
(3)当x=0,f(0)=-2<0恒成立,a∈R,
当0<x≤1时,f(x)<0恒成立,故|x-a|<![]() 恒成立,
恒成立,
即x-![]() <a<x+
<a<x+![]() 恒成立.
恒成立.
令y1=x+![]() ,y1’=1-
,y1’=1-![]() ,
,
当0<x≤1时,y’<0,故y1是(0,1]上的单调减函数,
所以y1≤1+2=3,故a<3;
令y2=x-![]() ,y2’=1+
,y2’=1+![]() >0,
>0,
故y2是(0,1]上的单调增函数,
所以y2≤1-2=-1,故a>-1.
又a<1,综上所述,a的取值范围为(-1,1).

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
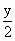 )是函数y=g(x)图象上的点.
)是函数y=g(x)图象上的点. ,D是由x轴和曲线y=f(x)及该曲线在点(1,0)处的切线所围成的封闭区域,则z=x-2y在D上的最大值为________.
,D是由x轴和曲线y=f(x)及该曲线在点(1,0)处的切线所围成的封闭区域,则z=x-2y在D上的最大值为________.