Question

如图，在棱长为1的正方体ABCD—A₁B₁C₁D₁中，M、N分别是线段BB₁、B₁C₁的中点，则直线MN和平面ACD₁的距离是（    ）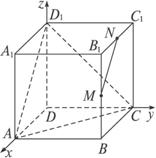

A.             B.                  C.               D.

Answer 1

答案：D  如下图，建立空间直角坐标系，则A（1，0，0），D₁（0，0，1），M（1，1，），N（，1，1），C（0，1，0）.

所以=(-1,0,1),=(-,0,).

所以=.又直线AD₁与MN不重合,所以∥.又MN平面ACD₁,

所以MN∥面ACD₁.

因为=(-1,0,1),=(0,1,-1),=(-1,1,0),

设平面ACD₁的法向量n=(x,y,z),

则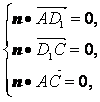所以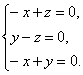

所以x=y=z.令x=1,则n=(1,1,1).

又因为=（1，1，）-（1，0，0）=（0，1，），

所以||=.

所以cos〈n,〉=.

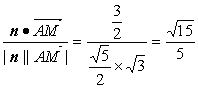所以点M到平面ACD₁的距离为||×cos〈n,〉=.