题目内容
已知角A是三角形的一个内角,若tanA=
(x<-1),则sinA的值为( )
| 2x |
| x2-1 |
分析:设t=-x,得到x=-t,代入已知的等式中变形后,利用万能公式表示出sinA,将t=-x代入,计算即可得到结果.
解答:解:设t=-x,可得x=-t,tanA=
=
=
,
∴sinA=
=
.
故选C
| 2x |
| x2-1 |
| -2t |
| t2-1 |
| 2t |
| 1-t2 |
∴sinA=
| 2t |
| 1+t2 |
| -2x |
| x2+1 |
故选C
点评:此题考查了万能公式,以及同角三角函数间的基本关系,万能公式为设t=
,则有tanA=
,sinA=
,cosA=
(A≠2kπ+π,k∈Z),熟练掌握万能公式是解本题的关键.
| A |
| 2 |
| 2t |
| 1-t2 |
| 2t |
| 1+t2 |
| 1-t2 |
| 1+t2 |

练习册系列答案
相关题目
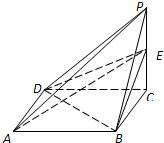
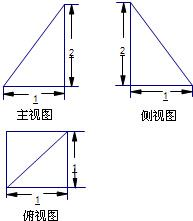
 (3)试探究在DE上是否存在点Q,使得AQ
(3)试探究在DE上是否存在点Q,使得AQ