题目内容
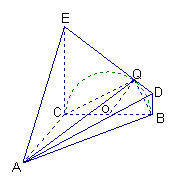
已知几何体A―BCED的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
(1)求此几何体的体积V的大小;
(2)求异面直线DE与AB所成角的余弦值;
 (3)试探究在DE上是否存在点Q,使得AQ
(3)试探究在DE上是否存在点Q,使得AQ![]() BQ并说明理由(一、二、五中必做,其它学校选做).
BQ并说明理由(一、二、五中必做,其它学校选做).
解析:(1)由该几何体的三视图知![]() 面
面![]() ,且EC=BC=AC=4 ,BD=1,
,且EC=BC=AC=4 ,BD=1,
 ∴
∴![]()
∴![]() .
.
即该几何体的体积V为16. -----------3分
(2)解法1:过点B作BF//ED交EC于F,连结AF,
则∠FBA或其补角即为异面直线DE与AB所成的角.-------5分
在△BAF中,∵AB=![]() ,BF=AF=
,BF=AF=![]() .
.
∴![]()
![]() .
.
即异面直线DE与AB所成的角的余弦值为![]() .------------------------------------------7分
.------------------------------------------7分
 解法2:以C为原点,以CA,CB,CE所在直线为x,y,z轴建立空间直角坐标系.
解法2:以C为原点,以CA,CB,CE所在直线为x,y,z轴建立空间直角坐标系.
则A(4,0,0),B(0,4,0),D(0,4,1),E(0,0,4)
∴![]() ,∴
,∴![]()
∴异面直线DE与AB所成的角的余弦值为![]() .
.
(3)解法1:在DE上存在点Q,使得AQ![]() BQ.--------------------------------------------------8分
BQ.--------------------------------------------------8分
取BC中点O,过点O作OQ⊥DE于点Q,则点Q满足题设.
连结EO、OD,在Rt△ECO和Rt△OBD中
∵![]()
![]() ∴
∴![]() ∽
∽![]() ∴
∴![]()
 ∵
∵![]() ∴
∴![]() ∴
∴![]() .-----------------10分
.-----------------10分
∵![]() ,
,![]()
∴![]()
∴以O为圆心、以BC为直径的圆与DE相切.切点为Q
∴![]()
∵![]() 面
面![]() ,
,![]() 面
面![]() ∴
∴![]() ∴
∴![]() 面
面![]()
∵![]() 面ACQ w.w.w.k.s.5.u.c.o.m
面ACQ w.w.w.k.s.5.u.c.o.m ![]()
∴![]() .-------------------------------------------------------------------------12分
.-------------------------------------------------------------------------12分
解法2: 以C为原点,以CA,CB,CE所在直线为x,y,z轴建立空间直角坐标系.
设满足题设的点Q存在,其坐标为(0,m,n),则![]()
![]() ,
,![]()
∵AQ![]() BQ ∴
BQ ∴![]() ----------------------------①
----------------------------①
∵点Q在ED上,∴存在![]()
![]() 使得
使得![]()
∴![]()
![]() -----------②
-----------②
②代入①得![]() ,解得
,解得![]()
∴满足题设的点Q存在,其坐标为![]()

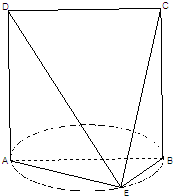 如图,已知四边形ABCD是边长为4cm的正方形,直线AD垂直于以AB为直径的圆所在的平面,点E是该圆上异于A,B的一点,连接AE、BE、DE、CE.
如图,已知四边形ABCD是边长为4cm的正方形,直线AD垂直于以AB为直径的圆所在的平面,点E是该圆上异于A,B的一点,连接AE、BE、DE、CE. 如图,已知四边形ABCD是边长为4cm的正方形,直线AD垂直于以AB为直径的圆所在的平面,点E是该圆上异于A,B的一点,连接AE、BE、DE、CE.
如图,已知四边形ABCD是边长为4cm的正方形,直线AD垂直于以AB为直径的圆所在的平面,点E是该圆上异于A,B的一点,连接AE、BE、DE、CE.