题目内容
已知点M是圆C:x2+y2=2上的一点,且MH⊥x轴,H为垂足,点N满足![]() =
=![]()
![]() ,记动点N的轨迹为曲线E.
,记动点N的轨迹为曲线E.
(1)求曲线E的方程;
(2)若AB是曲线E的长为2的动弦,O为坐标原点,求△AOB面积S的最大值.
[解析] (1)设N(x,y),M(x′,y′),则由已知得,x′=x,y′=![]() y,
y,
代入x2+y2=2得,x2+2y2=2.
所以曲线E的方程为![]() +y2=1.
+y2=1.
(2)因为线段AB的长等于椭圆短轴的长,要使三点A、O、B能构成三角形,则弦AB不能与x轴垂直,故可设直线AB的方程为y=kx+m,
由 消去y并整理得,
消去y并整理得,
(1+2k2)x2+4kmx+2m2-2=0.
设A(x1,y1),B(x2,y2),
又Δ=16k2m2-4(1+2k2)(2m2-2)>0,
所以x1+x2=-![]() ,x1x2=
,x1x2=![]() ,
,
因为|AB|=2,
所以![]() =2,
=2,
即(1+k2)[(x2+x1)2-4x1x2]=4,
所以(1+k2)[(-![]() )2-
)2-![]() ]=4,
]=4,
即m2=![]() ,
,
因为k2≥0,所以![]() ≤m2<1.
≤m2<1.
又点O到直线AB的距离h=![]() ,
,
因为S=![]() |AB|·h=h,
|AB|·h=h,
所以S2=h2=![]() =
=![]() .
.
令S2=u,1+k2=t,则t≥1,∴1+2k2=2t-1,
∴S2=![]() ,即u=
,即u=![]() ,u′=
,u′=![]() ≤0,
≤0,
∴u=![]() 在[1,+∞)上单调递减,
在[1,+∞)上单调递减,
∴t=1时,umax=![]() ,
,
即S2≤![]() ,∴0<S≤
,∴0<S≤![]() ,即S的最大值为
,即S的最大值为![]() .
.

练习册系列答案
相关题目
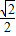 MH,记动点N的轨迹为曲线E.
MH,记动点N的轨迹为曲线E.