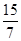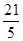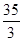题目内容
(本小题满分10分)选修4—1: 几何证明选讲
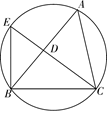
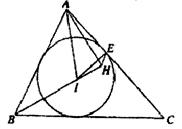
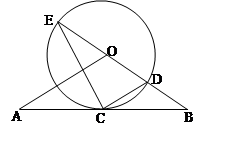
如图,已知 与圆
与圆 相切于点
相切于点 ,经过点
,经过点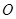 的割线
的割线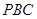 交圆
交圆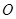 于点
于点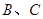 ,
,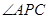 的平分线分别交
的平分线分别交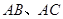 于点
于点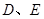 .
.
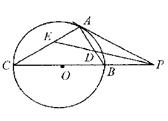
(1)证明: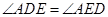 ;
;
(2)若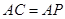 ,求
,求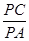 的值.
的值.
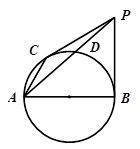
如图,已知
 与圆
与圆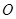 相切于点
相切于点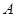 ,经过点
,经过点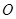 的割线
的割线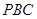 交圆
交圆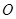 于点
于点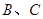 ,
,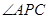 的平分线分别交
的平分线分别交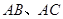 于点
于点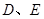 .
.
(1)证明:
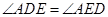 ;
;(2)若
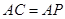 ,求
,求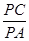 的值.
的值. (1)见解析;(2)  =
=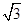 .
.
 =
=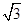 .
.本试题主要是考查了三角形的相似和圆内的性质的综合运用。
(1)因为结合切割线定理和弦切角定理可知角的相等,进而得到结论。
(2)由(1)知∠BAP=∠C, 又 ∵∠APC=∠BPA,
∴△APC∽△BPA并结合由三角形内角和定理可知,∠APC+∠C+∠CAP=180°可知在Rt△ABC中,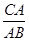 =
=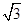 ,得到求解。
,得到求解。
解:(1)∵ PA是切线,AB是弦,
∴∠BAP=∠C,
又 ∵∠APD=∠CPE, ∴∠BAP+∠APD=∠C+∠CPE,
∵∠ADE=∠BAP+∠APD,
∠AED=∠C+∠CPE,
∴∠ADE=∠AED.
(2)由(1)知∠BAP=∠C, 又 ∵∠APC=∠BPA,
∴△APC∽△BPA, ∴ ,
,
∵ AC="AP," ∴∠APC=∠C=∠BAP,
由三角形内角和定理可知,∠APC+∠C+∠CAP=180°,
∵ BC是圆O的直径,∴∠BAC="90°," ∴∠APC+∠C+∠BAP=180°-90°=90°,
∴∠C=∠APC=∠BAP=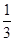 ×90°=30°.
×90°=30°.
在Rt△ABC中,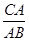 =
=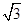 , ∴
, ∴ =
=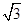 .
.
(1)因为结合切割线定理和弦切角定理可知角的相等,进而得到结论。
(2)由(1)知∠BAP=∠C, 又 ∵∠APC=∠BPA,
∴△APC∽△BPA并结合由三角形内角和定理可知,∠APC+∠C+∠CAP=180°可知在Rt△ABC中,
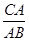 =
=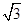 ,得到求解。
,得到求解。解:(1)∵ PA是切线,AB是弦,
∴∠BAP=∠C,
又 ∵∠APD=∠CPE, ∴∠BAP+∠APD=∠C+∠CPE,
∵∠ADE=∠BAP+∠APD,
∠AED=∠C+∠CPE,
∴∠ADE=∠AED.
(2)由(1)知∠BAP=∠C, 又 ∵∠APC=∠BPA,
∴△APC∽△BPA, ∴
 ,
, ∵ AC="AP," ∴∠APC=∠C=∠BAP,
由三角形内角和定理可知,∠APC+∠C+∠CAP=180°,
∵ BC是圆O的直径,∴∠BAC="90°," ∴∠APC+∠C+∠BAP=180°-90°=90°,
∴∠C=∠APC=∠BAP=
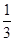 ×90°=30°.
×90°=30°. 在Rt△ABC中,
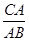 =
=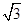 , ∴
, ∴ =
=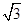 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 经过⊙
经过⊙ 上的点
上的点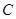 ,并且
,并且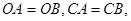 ⊙
⊙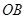 于
于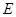 ,
,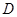 ,连接
,连接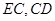 .
.
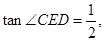 ⊙
⊙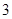 ,求
,求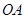 的长.
的长.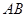 是⊙
是⊙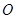 的一条弦,点
的一条弦,点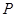 为
为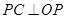 ,
,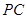 交⊙
交⊙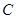 ,若
,若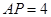 ,
,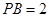 ,则
,则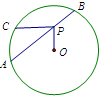
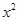 -7
-7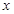 +12=0的两根,则
+12=0的两根,则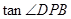 =_________。
=_________。
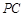 切⊙
切⊙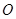 于点
于点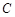 ,割线
,割线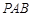 经过圆心
经过圆心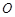 ,弦
,弦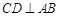 于点
于点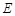 .已知⊙
.已知⊙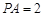 ,则
,则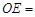 .
.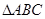 的
的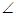
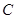 的平分线
的平分线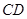 延长后交圆于点
延长后交圆于点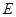 , 连接
, 连接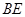 , 已知
, 已知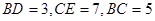 , 则线段
, 则线段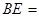 ( )
( )