题目内容
12.已知数列{an}的前n项和Sn=2n2+3n.(1)求数列{an}的通项公式;
(2)25是否是该数列中的项,若是,是第几项?
分析 (1)利用递推关系即可得出.
(2)令an=25,解出即可判断出结论.
解答 解:(1)∵数列{an}的前n项和Sn=2n2+3n.
∴n=1时,a1=S1=5;
当n≥2时,an=Sn-Sn-1=2n2+3n-[2(n-1)2+3(n-1)]=4n+1.
∴an=4n+1.
(2)假设4n+1=25,解得n=6.
∴25是否是该数列中的第6项.
点评 本题考查了等差数列的通项公式及其前n项和公式、递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
2.已知点F1与点F2是双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{10}$=1的左、右焦点,点P在直线l:x-$\sqrt{3}$y+8+2$\sqrt{3}$=0上,当∠F1PF2取最大值时,$\frac{|P{F}_{1}|}{|P{F}_{2}|}$的比值是( )
| A. | $\sqrt{2}+1$ | B. | $\sqrt{3}+1$ | C. | $\sqrt{2}-1$ | D. | $\sqrt{3}-1$ |
20.已知实数x、y满足$\left\{\begin{array}{l}{x-y+2≥0}\\{x+2y+2≥0}\\{4x-y-10≤0}\end{array}\right.$,z=kx+y(k∈R)仅在(4,6)处取得最大值,则k的取值范围是( )
| A. | k>1 | B. | k>-1 | C. | k<-$\frac{1}{2}$ | D. | k<-4 |
13.直线$\left\{\begin{array}{l}x=5-3t\\ y=3+\sqrt{3}t\end{array}\right.$(为参数)的倾斜角为( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
14.设A1,A2分别为双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左右顶点,若双曲线上存在点M使得两直线斜率${k_{M{A_1}}}{k_{M{A_2}}}<2$,则双曲线C的离心率的取值范围为( )
| A. | $(0,\sqrt{3})$ | B. | $(1,\sqrt{3})$ | C. | $(\sqrt{3},+∞)$ | D. | (0,3) |
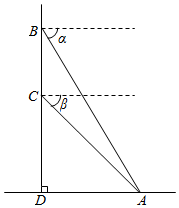 如图,山顶上有一座电视塔,在塔顶B处测得地面上一点A的俯角α=60°,在塔底C处测得点A的俯角β=45°,已知塔高60m,则山高为30($\sqrt{3}$+1).
如图,山顶上有一座电视塔,在塔顶B处测得地面上一点A的俯角α=60°,在塔底C处测得点A的俯角β=45°,已知塔高60m,则山高为30($\sqrt{3}$+1).