Question

已知焦点在x轴上的双曲线C的两条渐近线过坐标原点，且两条渐近线与以点A(0，)为圆心，1为半径的圆相切，又知C的一个焦点与A关于直线y=x对称.

(1)求双曲线C的方程；

(2)设直线y=mx+1与双曲线C的左支交于A、B两点，另一直线l经过M(-2,0)及AB的中点，求直线l在y轴上的截距b的取值范围.

Answer 1

解：(1)设双曲线C的渐近线方程为y=kx,即kx-y=0.

∵该直线与圆x²+(y-)²=1相切，∴双曲线C的两条渐近线方程为y=±x.

    故设双曲线C的方程为-=1.

    又双曲线C的一个焦点为(,0),∴2a²=2,a²=1.∴双曲线C的方程为x²-y²=1.

(2)由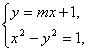得(1-m²)x²-2mx-2=0.

    令f(x)=(1-m²)x²-2mx-2,

    直线与双曲线左支交于两点等价于方程f(x)=0在(-∞,0)上有两个不等实根.

    因此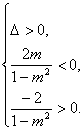

    解得1＜m＜.

    又AB的中点坐标为(,),

∴直线l的方程为y=(x+2).

    令x=0,得b=.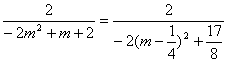

∵m∈(1,),

∴-2(m-)²+∈(-2+,1).

∴b∈(-∞,-2-)∪(2,+∞).