题目内容
已知双曲线C1:
-
=1的左准线为l,左、右焦点分别为F1、F2,抛物线C2的准线为l焦点是F2,若C1与C2的一个交点为P,则|PF2|的值等于( )
| x2 |
| 16 |
| y2 |
| 9 |
| A、40 | B、32 | C、8 | D、4 |
分析:由题设条件知抛弧线C2的准线为 x=-
,焦点为(5,0),即 p=5-(-
)=
,抛物线的顶点的横坐标为
,设P的坐标为(m,n),m>
,对于抛物线而言,|PF2|=m-(-
)=m+
.对于双曲线,e1=
=
,|PF2|=
(m-
),由此能求出|PF2|的值.
| 16 |
| 5 |
| 16 |
| 5 |
| 41 |
| 5 |
| 9 |
| 10 |
| 9 |
| 10 |
| 16 |
| 5 |
| 16 |
| 5 |
| c |
| a |
| 5 |
| 4 |
| 5 |
| 4 |
| 16 |
| 5 |
解答:解:由题设条件知a=4,b=3,c=5,
∴左准线l为 x=-
,右准线为 x=
,右焦点为F2(5,0).
∴抛弧线C2的准线为 x=-
,焦点为(5,0),即 p=5-(-
)=
,
焦点到准线的垂线段的中点,即为抛物线的顶点.该点的横坐标为
=
,可见P点必在双曲线的右半支,
设P的坐标为(m,n),因此m>
,
对于抛物线而言,e2=1,即|PF2|=m-(-
)=m+
.
对于双曲线,e1=
=
,
P到F2的距离与P到右准线的距离之比为e1
即
=e1,即|PF2|=
(m-
),
即 m+
=
(m-
)
即得m=
,
将其代入|PF2|=m+
中,即|PF2|=
=32.
故选B.
∴左准线l为 x=-
| 16 |
| 5 |
| 16 |
| 5 |
∴抛弧线C2的准线为 x=-
| 16 |
| 5 |
| 16 |
| 5 |
| 41 |
| 5 |
焦点到准线的垂线段的中点,即为抛物线的顶点.该点的横坐标为
5-
| ||
| 2 |
| 9 |
| 10 |
设P的坐标为(m,n),因此m>
| 9 |
| 10 |
对于抛物线而言,e2=1,即|PF2|=m-(-
| 16 |
| 5 |
| 16 |
| 5 |
对于双曲线,e1=
| c |
| a |
| 5 |
| 4 |
P到F2的距离与P到右准线的距离之比为e1
即
| |PF2| | ||
m-
|
| 5 |
| 4 |
| 16 |
| 5 |
即 m+
| 16 |
| 5 |
| 5 |
| 4 |
| 16 |
| 5 |
即得m=
| 144 |
| 5 |
将其代入|PF2|=m+
| 16 |
| 5 |
| 160 |
| 5 |
故选B.
点评:本题考查圆锥曲线的综合应用,解题时要认真审题,注意公式的合理运用.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
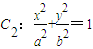 有公共焦点F1F2,点
有公共焦点F1F2,点 是它们的一个公共点.
是它们的一个公共点.