题目内容
已知双曲线C1:x2-
=1,双曲线C2与双曲线C1有相同的渐近线且经过点(
,2)
(1)求双曲线C2的标准方程;
(2)若直线y=x-1与双曲线C2的两渐近线相交于A,B,求
•
的值.
| y2 |
| 4 |
| 3 |
(1)求双曲线C2的标准方程;
(2)若直线y=x-1与双曲线C2的两渐近线相交于A,B,求
| OA |
| OB |
分析:(1)设与x2-
=1有共同渐近线的双曲线方程为x2-
=λ,代入已知点可得λ,可得方程;
(2)先得双曲线C2的两渐近线方程,联立所给直线可得得点A、B的坐标,进而可得向量的坐标,由数量积的定义可得.
| y2 |
| 4 |
| y2 |
| 4 |
(2)先得双曲线C2的两渐近线方程,联立所给直线可得得点A、B的坐标,进而可得向量的坐标,由数量积的定义可得.
解答:解:(1)设与x2-
=1有共同渐近线的双曲线方程为x2-
=λ,
把点(
,2)代入可得3-1=λ,即λ=2,
∴双曲线C2的标准方程为x2-
=2,即
-
=1;
(2)可得双曲线C2的两渐近线为:y=±
x=±2x
联立
可解得
,同理联立
可解得
,
故可得点A、B分别为(1,2)(
,
),
故
•
=1×
+2×
=
| y2 |
| 4 |
| y2 |
| 4 |
把点(
| 3 |
∴双曲线C2的标准方程为x2-
| y2 |
| 4 |
| x2 |
| 2 |
| y2 |
| 8 |
(2)可得双曲线C2的两渐近线为:y=±
2
| ||
|
联立
|
|
|
|
故可得点A、B分别为(1,2)(
| 1 |
| 3 |
| 2 |
| 3 |
故
| OA |
| OB |
| 1 |
| 3 |
| 2 |
| 3 |
| 5 |
| 3 |
点评:本题考查双曲线的标准方程,涉及平面向量数量积的运算,属中档题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
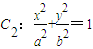 有公共焦点F1F2,点
有公共焦点F1F2,点 是它们的一个公共点.
是它们的一个公共点.